Expresiones algebraicas
Las expresiones algebraicas son expresiones matemáticas que pueden contener números, letras, símbolos y operadores aritméticos. Sirven para representar una relación entre elementos de forma simplificada y establecer igualdades. Sin las expresiones algebraicas, algunas fórmulas serían muy complicadas de comunicar a otras personas.
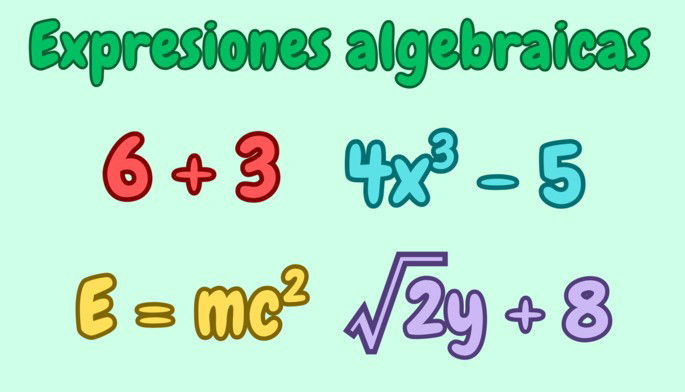
Una expresión algebraica puede ser tan sencilla como una suma de dos números, 6 + 3, o fórmulas con diversas variables y términos como:
Las expresiones algebraicas nos sirven para realizar cálculos o entender rápidamente qué tipo de operaciones debemos realizar. Las utilizamos constantemente en el día a día, desde la compra de productos hasta la solución de problemas en ciencias e ingeniería que requieren de conocimientos matemáticos.
Por ejemplo, es más fácil escribir:
2x + √y - 7 = z2 + z/4
Que tener que decir: dos multiplicado por la variable x más la raíz de y menos siete es igual que z al cuadrado más z dividido entre cuatro. Por tanto, la comunicación es mucho más rápida y entendible a través de las expresiones algebraicas.
En resumen, las ventajas de utilizar las expresiones algebraicas son:
- Emplear un lenguaje más legible para representar operaciones matemáticas.
- Resolver problemas que requieran de lenguaje matemático.
- Establecer con facilidad las relaciones que se dan entre elementos.
- Plantear ecuaciones y funciones con una o más variables.
Partes de una expresión algebraica
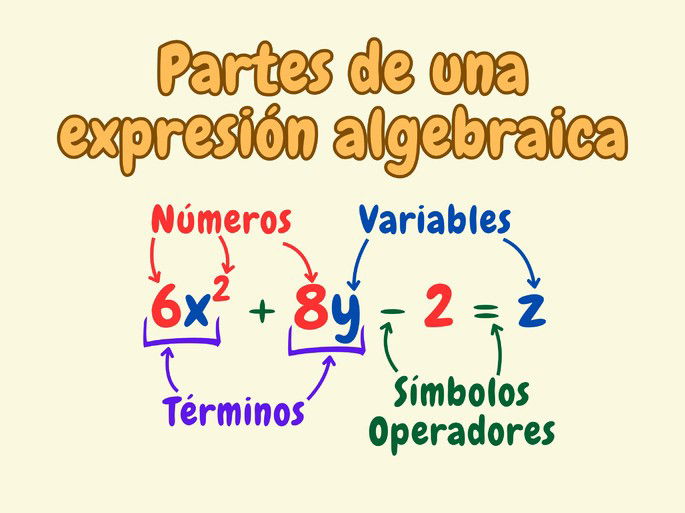
Cada expresión algebraica se compone de una o más partes: de números, letras, términos, y símbolos y operadores aritméticos.
Números: los números expresan cantidades concretas con los que podemos trabajar para realizar cálculos, sean sumas, restas, multiplicaciones, divisiones o exponentes. Los números aparecen como términos independientes o como coeficientes que multiplican variables.
Ejemplos de números son: 1, 5, 10, 843 o 11,6374.
Letras: se emplean para representar variables o incógnitas en una expresión algebraica, que bien pueden tener un valor conocido o desconocido. Aquí se incluyen constantes simbolizadas con una letra, como el número pi (π), el número de Euler (e) o la constante de gravitación universal (G).
Otras letras comunes que se usan son x y z, que simbolizan variables que pueden tomar distintos valores.
Términos: es un elemento compuesto por un número, una letra o una combinación de estas. Cada término se separa de otro mediante sumas y restas.
Símbolos y operadores aritméticos: los operadores indican las sumas, restas, multiplicaciones y divisiones que se realizan entre números y variables. Además de los operadores, se emplean diversos símbolos matemáticos para realizar una gran variedad de operaciones matemáticas.
Algunos ejemplos de símbolos son el signo de igualdad (=), la raíz cuadrada (√), los símbolos de mayor o menor que (> y <), el porcentaje (%) o la sumatoria (∑).
Otros símbolos son los paréntesis, corchetes o llaves para agrupar diferentes operaciones dentro de la expresión algebraica. Emplear estos símbolos nos ayuda a entender qué operaciones debemos realizar primero para operar de forma ordenada.
Por último, aquí también se incluyen los signos, que indican si un número o variable es positivo (con signo +) o negativo (con signo -).
Vea también Símbolos matemáticos.
Ejemplos de expresiones algebraicas
A continuación mostramos varios ejemplos de expresiones algebraicas y la forma en que estas se leen, para evidenciar que es más fácil escribir las expresiones que describirlas usando palabras:
| Expresión algebraica | Cómo se lee la expresión |
|---|---|
| 2x + 6 | El doble de un número más seis. |
| x2 + x/2 | El cuadrado de un número más su mitad. |
| x/3 - √5 | El tercio de un número menos la raíz cuadrada de cinco. |
| (3 x 5) + (8 x 2) | La suma de los resultados de tres por cinco y ocho por dos. |
| x3 + 4x2 - 6x + 3 = 0 | El cubo de un número más cuatro por el cuadrado de dicho número, menos seis veces dicho número más tres es igual a cero. |
| x + y = 15 - z2 | La suma de dos números diferentes es igual a quince menos el cuadrado de un tercer número. |
| (3√x + 4y) / y3 | La raíz cúbica de un número más el cuádruple de otro número dividido por el cubo de este segundo número. |
| (x) + (x+1) + (x+2) + (x+3) | La suma de cuatro números consecutivos. |
| xy + x2 - y/4 = 12 + √z | El producto de dos números más el cuadrado del primer número menos la cuarta parte del segundo número es igual a 12 más la raíz cuadrada de un tercer número. |
Como bien pudiste ver, sin las expresiones algebraicas, algunas operaciones matemáticas resultarían complicadas de entender o de comunicar.
Clasificación de las expresiones algebraicas
Los números, las letras y los operadores se pueden combinar de infinitas maneras para expresar operaciones matemáticas. A grandes rasgos, podemos clasificar las expresiones algebraicas de dos formas: en monomios y en polinomios.
Monomios
Son expresiones algebraicas que solo presentan un término, usualmente compuestos por una sola variable o una variable con un coeficiente y un exponente.
Ejemplos de monomios son:
Polinomios
Son aquellas expresiones algebraicas que contienen dos o más términos separados por sumas y restas. Dentro de los polinomios podemos hablar de los binomios, que presentan dos términos, y los trinomios, que presentan tres términos, pero también hay expresiones con más términos.
Algunos ejemplos de polinomios son:
Asimismo, los polinomios también se clasifican según el grado indicado por los exponentes que elevan las variables:
Vea también Polinomio, Ecuación de primer grado y Ecuaciones de segundo grado.
Otros tipos de expresiones algebraicas
Además de monomios y polinomios, las expresiones algebraicas se denominan de una u otra forma según los elementos que hay en la expresión y la relación establecida entre ellas.
Por ejemplo, un tipo de expresiones algebraicas son las ecuaciones o igualdades, como:
Otro caso son las funciones, como:
Además, las expresiones algebraicas se pueden clasificar según el número de variables que contenga:
Vea también Álgebra y Ecuaciones.
Cómo citar: Rhoton, Stephen (28/05/2025). "Expresiones algebraicas". En: Significados.com. Disponible en: https://www.significados.com/expresiones-algebraicas/ Consultado:










