Ecuación de primer grado
Una ecuación de primer grado es una igualdad matemática con una o más incógnitas. Dichas incógnitas deben ser despejadas o resueltas para encontrar el valor numérico de la igualdad.
Las ecuaciones de primer grado reciben este nombre porque sus variables (incógnitas) están elevadas a la primera potencia (X1), que suele representarse solo con una X.
Del mismo modo, el grado de la ecuación indica el número de soluciones posibles. Por lo tanto, una ecuación de primer grado (también llamada ecuación lineal) solo tiene una solución.
Ecuación de primer grado con una incógnita
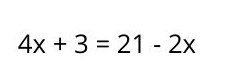
Para resolver ecuaciones lineales con una incógnita, deben ejecutarse algunos pasos:
1. Agrupar los términos con X hacia el primer miembro y los que no llevan X al segundo miembro. Es importante recordar que cuando un término pasa al otro lado de la igualdad, su signo cambia (si es positivo pasa a ser negativo y viceversa).
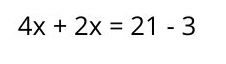
3. Se realizan las operaciones respectivas en cada miembro de la ecuación. En este caso, corresponde una suma en uno de los miembros y una resta en el otro, lo que da como resultado:
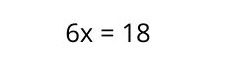
4. Se despeja la X, pasando el término que tiene adelante al otro lado de la ecuación, con signo opuesto. En este caso, el término está multiplicando, así que ahora pasa a dividir.
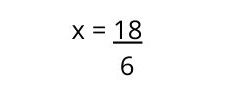
5. Se resuelve la operación para conocer el valor de X.
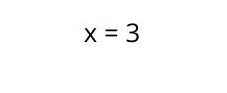
Entonces, la resolución de la ecuación de primer grado quedaría de la siguiente manera:
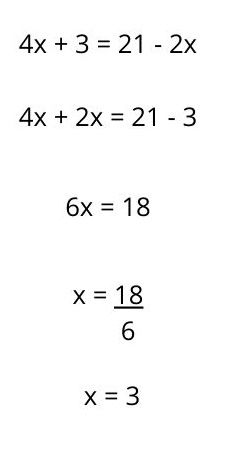
Ecuación de primer grado con paréntesis
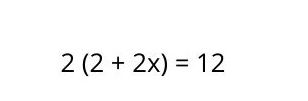
En una ecuación lineal con paréntesis, estos signos nos indican que todo lo que está dentro de ellos debe ser multiplicado por el número que tienen adelante. Este es el paso a paso para resolver ecuaciones de este tipo:
1. Multiplicar el término por todo lo que está dentro del paréntesis, con lo cual la ecuación quedaría de la siguiente forma:
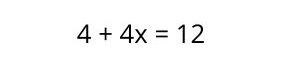
2. Una vez que se ha resuelto la multiplicación, queda una ecuación de primer grado con una incógnita, que se resuelve como hemos visto anteriormente, es decir, agrupando los términos y haciendo las operaciones respectivas, cambiando los signos de aquellos términos que pasen al otro lado de la igualdad:
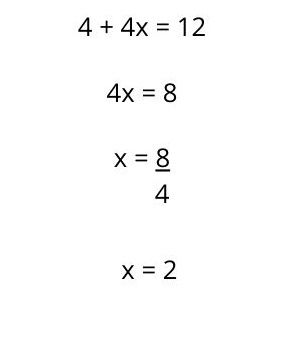
Ecuación de primer grado con fracciones y paréntesis
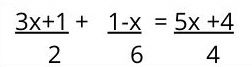
Aunque las ecuaciones de primer grado con fracciones parecen complicadas, realidad solo llevan algunos pasos extras antes de convertirse en una ecuación básica:
1. En primer lugar, hay que obtener el mínimo común múltiplo de los denominadores (el múltiplo más pequeño que sea común a todos los denominadores presentes). En este caso, el mínimo común múltiplo es 12.
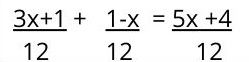
2. Luego, se divide el denominador común entre cada uno de los denominadores originales. El producto resultante va a multiplicar al numerador de cada fracción, los cuales ahora van entre paréntesis.
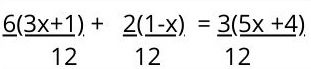
3. Se multiplican los productos por cada uno de los términos que se encuentran dentro de los paréntesis, tal y como se haría en una ecuación de primer grado con paréntesis.
Al culminar, se procede a simplificar la ecuación eliminando los denominadores comunes:
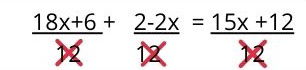
El resultado es una ecuación de primer grado con una incógnita, que se resuelve de la manera habitual:
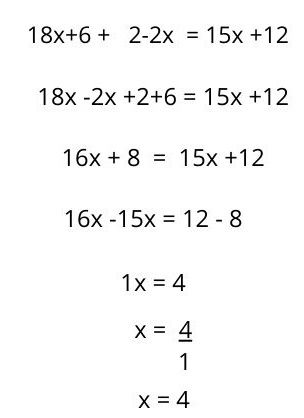
Ver también:
Cómo citar: (20/12/2019). "Ecuación de primer grado". En: Significados.com. Disponible en: https://www.significados.com/ecuacion-de-primer-grado/ Consultado: