Ley de Faraday

Stephen Rhoton
Stephen Rhoton
Graduado en Ingeniería de Sistemas Biológicos

La ley de Faraday o de Lenz-Faraday nos explica que la tensión inducida en un circuito eléctrico es directamente proporcional a la variación del campo magnético que lo atraviesa.

Esta ley fue formulada por el físico y químico británico Michael Faraday en 1831, después de realizar diversos experimentos con circuitos eléctricos durante el siglo XIX.

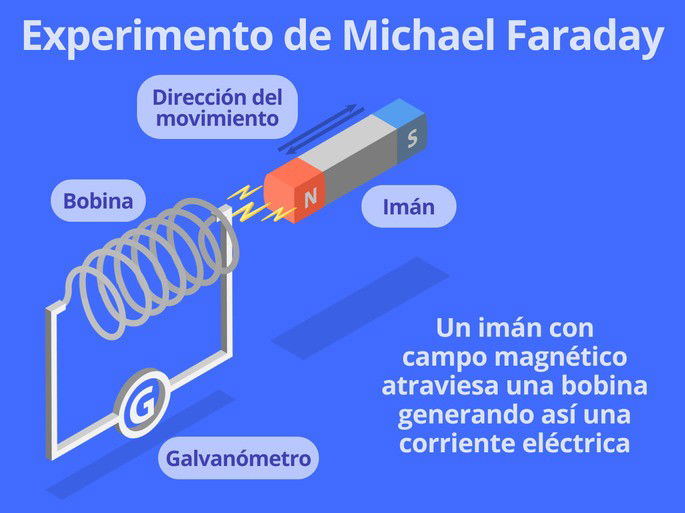
Experimento de Michael Faraday con el que enunció la ley de Faraday

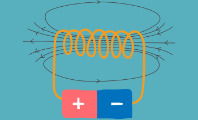
Faraday descubrió el concepto de la fuerza electromotriz y la inducción electromagnética sirviéndose de varios experimentos. En uno de ellos empleó un imán y una bobina enrollada sobre un tubo. Al introducir el imán en el interior del tubo, observó que el voltaje medido entre los dos extremos de la bobina aumentaba conforme el imán se acercaba al centro.

Además, se fijó que el voltaje en un extremo del tubo era opuesto a cuando movía el imán hacia el otro extremo. Con ello concluyó que la presencia de un campo magnético induce una corriente eléctrica, y su posición o movimiento también influye en la dirección de la corriente.

Este descubrimiento tuvo gran importancia, ya que nos permitió entender cómo construir mejor los generadores eléctricos, transformadores y bobinas de ignición para que fueran más eficaces. Asimismo, todo lo relacionado con la transmisión inalámbrica (televisión, radio, satélites) se vale de la ley de Faraday.

La ley de Faraday está ligada con la ley de Lenz, la cual indica que toda tensión inducida circula en sentido opuesto a la variación del campo magnético que indujo dicha tensión. A continuación ilustramos las leyes con sus fórmulas.

Fórmulas de la ley de Faraday

La fórmula principal de la ley de Faraday que relaciona la variación del campo magnético con la corriente inducida por él es:

Ɛ igual menos fracción numerador d ϕ subíndice M entre denominador d t fin fracción

En que:

  • Ɛ (epsilon) es la fuerza electromotriz o FEM, medido en voltios (V);
  • dϕM es la variación del flujo magnético, usualmente medido en Weber (Wb);
  • dt es la variación del tiempo, medido en segundos (s).

Es decir, acorde a esta fórmula, la fuerza electromotriz (Ɛ) que se induce en un circuito cerrado viene afectada por el cambio de flujo magnético (dϕM) a lo largo del tiempo (dt). Cabe aclarar que la fuerza electromotriz es una diferencia de potencial, no una fuerza literalmente hablando.

El signo negativo "−" en la fórmula nos muestra que el sentido de la corriente inducida se opone al flujo magnético. Esto proviene de la ley de Lenz.

Como las variables del flujo magnético y tiempo son variaciones, otra manera de representar ambas variables es:

  • dϕM = ϕM final - ϕM inicial
  • dt = tfinal - tinicial

A su vez, el flujo magnético ϕM es igual al producto del campo magnético (B) y la superficie donde actúa dicho campo (S). Por tanto, el flujo magnético es ϕM = B · S.

A partir de la anterior relación, la ecuación se puede reescribir de otra forma:

Ɛ igual menos fracción numerador d entre denominador d t fin fracción integral subíndice S B con flecha derecha encima por d S con flecha derecha encima

Bobina con varias espiras

Las fórmulas anteriores se aplican solamente a circuitos cerrados o bobinas de una sola espira. Cuando la bobina tiene varias espiras, la fórmula es:

V subíndice Ɛ igual menos N fracción numerador d ϕ subíndice M entre denominador d t fin fracción

Donde:

  • VƐ es la tensión o fuerza electromotriz inducida, en voltios (V);
  • N es el número de espiras, sin unidades;
  • dϕM es la variación del flujo magnético, usualmente medido en Weber (Wb);
  • dt es la variación del tiempo, medido en segundos (s).

Esto es debido a que cada espira contribuye con la misma fuerza electromotriz. Por tanto, la fórmula es casi la misma que la primera que presentamos en el artículo, con la diferencia de que añadimos el número de espiras o vueltas (N) como factor.

Vea también Electromagnetismo.

Ejemplos de la ley de Faraday

Aquí compartimos unos ejemplos en que se aplica la ley de Faraday.

Ejemplo 1

Sobre un circuito eléctrico se produce una variación de flujo magnético de 0,2 Wb durante medio segundo. ¿Cuál es la fuerza electromotriz inducida?

Respuesta: -0,4 V

Por un lado, el enunciado nos dice que la variación de flujo magnético, es de 0,2 Wb. Por el otro, nos pregunta qué fuerza electromotriz se induce cuando dicha variación ocurre en medio segundo, es decir, 0,5 s.

Como tenemos todos los valores necesarios, podemos aplicar la fórmula:

Ɛ igual menos fracción numerador d ϕ subíndice M entre denominador d t fin fracción igual menos fracción numerador 0 coma 2 espacio W b entre denominador 0 coma 5 espacio s fin fracción igual menos 0 coma 4 V

Por tanto, la fuerza electromotriz inducida fue de -0,4 voltios.

Ejemplo 2

Calcula la fuerza electromotriz inducida si en 5 segundos el flujo magnético cambió de 1 a 0,3 Weber.

Respuesta: 0,14 V

Aquí hemos de tener en cuenta de que hay un punto inicial y uno final. Nos dice que, en 5 segundos, el flujo magnético ha pasado de medir 1 Weber a tener un valor de 0,3 Weber. Esto sucede cuando se mueve el circuito o se desplaza el objeto que produce el campo magnético.

Por tanto, las variaciones de flujo magnético y tiempo son:

dϕM = (ϕM final - ϕM inicial) = 0,3 Wb - 1 Wb = -0,7 Wb

dt = (tfinal - tinicial) = 5 s - 0 s = 5 s

Calculadas las variables, aplicamos la fórmula:

Ɛ igual menos fracción numerador d ϕ entre denominador d t fin fracción igual menos fracción numerador paréntesis izquierdo menos 0 coma 7 espacio W b paréntesis derecho entre denominador 5 espacio s fin fracción igual 0 coma 14 espacio V

La respuesta es 0,14 voltios. Ten en cuenta que los signos son importantes para indicar que el flujo magnético y la fuerza electromotriz inducida tienen sentidos opuestos. Es por eso que, como la variación del flujo magnético es negativa, la fuerza electromotriz ha de ser positiva.

Ejemplo 3

El flujo magnético que atraviesa en tres segundos una bobina hasta llegar a su centro varía de 0,1 Weber a 0,6 Weber. ¿Cuál es la fuerza electromotriz inducida si la bobina tiene 28 espiras?

Respuesta: -4,67 V

En este ejemplo volvemos a tener un caso en que hay una variación del flujo magnético y el tiempo, pero con una diferencia clave: la bobina presenta 28 espiras.

Calculemos primero la variación total del flujo magnético y del tiempo. En este caso:

dϕM = (ϕM final - ϕM inicial) = 0,6 Wb - 0,1 Wb = 0,5 Wb

dt = (tfinal - tinicial) = 3 s - 0 s = 3 s

Calculadas las variables, ahora debemos aplicar la fórmula que incluye el número de espiras (N) en la fórmula:

V subíndice Ɛ igual menos N fracción numerador d ϕ subíndice M entre denominador d t fin fracción igual menos 28 por fracción numerador 0 coma 5 espacio W b entre denominador 3 espacio s fin fracción igual menos 4 coma 67 espacio fino V

La fuerza electromotriz inducida por el flujo magnético es de -4,67 voltios.

Enlaces a tener en cuenta:

Cómo citar: Rhoton, Stephen (23/10/2025). "Ley de Faraday". En: Significados.com. Disponible en: https://www.significados.com/ley-de-faraday/ Consultado:

Stephen Rhoton
Stephen Rhoton
Stephen se graduó en 2017 en Ingeniería de Sistemas Biológicos, y finalizó en 2020 los estudios del máster en Tecnologías Facilitadoras para la Industria Alimentaria y de Bioprocesos. Cursó ambos en EEAABB (Escuela de Ingeniería Agroalimentaria y de Biosistemas de Barcelona).
Otros contenidos que pueden ser de tu interés