Jerarquía de operaciones
La jerarquía de operaciones nos indica el orden en que debemos realizar las diferentes operaciones matemáticas de una ecuación o fórmula.
Es decir, nos ayuda a entender en qué orden podemos simplificar una ecuación que contiene diversos términos y operadores como las sumas, multiplicaciones o potencias. Si no seguimos esta jerarquía, nos arriesgaremos a completar operaciones matemáticas de forma incorrecta.
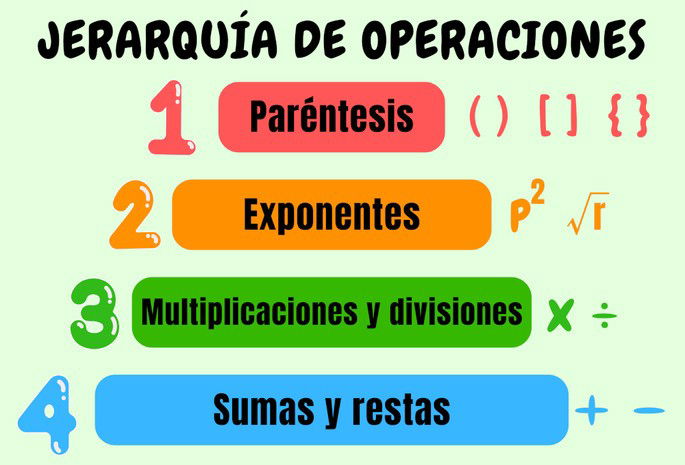
De forma resumida, los eslabones de la jerarquía o prioridad de operaciones son:
- Paréntesis
- Exponentes
- Multiplicaciones y divisiones
- Sumas y restas
Pongamos el siguiente ejemplo:
Hay bastantes cálculos a realizar, y por eso nos ayuda seguir una jerarquía. Primero, resolvemos las operaciones ubicadas entre paréntesis:
Proseguimos calculando los exponentes, es decir, la potencia y el radical:
El siguiente paso es realizar la multiplicación y división:
Terminamos con las sumas y restas, y con ello, obtenemos el resultado de la ecuación:
Además de esta jerarquía, se ha de tener en cuenta que las operaciones de un mismo nivel siguen un orden estricto de izquierda a derecha. Es decir, si primero tenemos una suma y luego una resta, resolvemos primero la suma, y luego la resta.
Veamos punto por punto la jerarquía de operaciones, y otros ejemplos para ilustrar.
1. Paréntesis
Cualquier operación matemática acotada entre paréntesis se ha de resolver primero, antes de proseguir con el resto de operaciones. Fíjate en estos ejemplos:
Cabe mencionar que las operaciones contenidas entre paréntesis siguen también una jerarquía de operaciones. Es por esa razón que, en el segundo ejemplo, primero resolvimos 2 x 16 antes de sumar 8.
Aunque solemos utilizar paréntesis, a veces se usan otros símbolos de agrupación para establecer una jerarquía de operaciones en este mismo nivel. Además, emplear diferentes símbolos ayuda en la legibilidad en operaciones largas.
Los tipos son:
- los paréntesis, ( );
- los corchetes, [ ];
- y las llaves, { }.
Abajo ilustramos con dos ejemplos la diferencia en claridad de una misma serie de operaciones matemáticas:
Vea también Operaciones combinadas.
2. Exponentes
Con exponentes nos referimos a las potencias, como 22, y radicales, como √8. Después de resolver todos los paréntesis, conviene calcular los exponentes que contenga la ecuación o fórmula.
Por ejemplo, en la siguiente operación:
Primero hemos de resolver la potencia y el radical, para entonces realizar la suma y la resta:
Ten en cuenta que si el radical contiene a su vez operaciones matemáticas, primero hemos de resolver dichas operaciones y luego calcular la raíz. Un ejemplo es el siguiente:
Vea también Leyes de los exponentes.
3. Multiplicaciones y divisiones
Siempre que haya términos multiplicándose o dividiéndose, se han de resolver primero dichas operaciones antes de cualquier suma o resta. Si no lo hacemos así, obtendremos resultados completamente distintos.
Para ilustrar esto, calculemos una ecuación de la forma correcta, y luego la incorrecta:
Como puedes ver en el ejemplo, calcular primero la suma antes de la multiplicación y división nos da un resultado incorrecto.
Ahora, si el numerador de una división consiste de varias operaciones matemáticas, se han de resolver antes de proceder con la división.
Fíjate en el siguiente ejemplo:
Como pudiste ver, primero se realizó la multiplicación en el numerador, seguido de la suma, y finalmente se resuelve la división.
Vea también Multiplicación, División y Propiedades de la multiplicación.
4. Sumas y restas
Las sumas y restas comprenden el último eslabón de la jerarquía de operaciones, lo que implica que serán la última operación a realizar en una ecuación o fórmula matemática.
En otras palabras, es necesario que calculemos todas las potencias, radicales, multiplicaciones y divisiones antes de realizar sumas y restas. Si no lo hacemos así, nos arriesgaremos a obtener resultados incorrectos en las operaciones matemáticas.
Hay tres excepciones que ya hemos mencionado en el artículo, pero que enumeraremos aquí para repasar:
- Si hay sumas y restas entre paréntesis, se han de resolver estas operaciones matemáticas antes de proceder con otras que se hallan fuera de los paréntesis.
- Si hay sumas y restas en el numerador de una división, se han de resolver estas operaciones matemáticas antes de calcular la división.
- Si hay sumas y restas dentro de un radical, es preciso hacer estas operaciones matemáticas para luego calcular la raíz.
Vea también Suma o adición, Resta o sustracción y Ley de los signos.
Ejemplos de práctica de jerarquía de operaciones
A continuación compartimos cinco ejercicios para practicar lo aprendido sobre la jerarquía de operaciones. Recuerda los niveles de la jerarquía:
- Paréntesis
- Exponentes
- Multiplicaciones y divisiones
- Sumas y restas
Ejercicio 1
Resuelve la siguiente operación:
4 + 6 x 2 − 25 ÷ 5 + 1
Ejercicio 2
Resuelve la siguiente operación:
Ejercicio 3
Resuelve la siguiente operación:
Ejercicio 4
Resuelve la siguiente operación:
Ejercicio 5
Resuelve la siguiente operación:
Cómo citar: (10/04/2025). "Jerarquía de operaciones". En: Significados.com. Disponible en: https://www.significados.com/jerarquia-de-operaciones/ Consultado: