Fracciones equivalentes
Las fracciones equivalentes son aquellas que representan una misma cantidad, pero que poseen numeradores y denominadores distintos. Es decir, obtenemos el mismo cociente cuando realizamos las divisiones entre los correspondientes numeradores y denominadores.

Pongamos el siguiente ejemplo:
Estas fracciones son distintas, pues contienen diferentes numeradores y denominadores. No obstante, son fracciones equivalentes. ¿Cómo sabemos eso? Si realizamos en cada caso la división entre el numerador y el denominador, veremos que el resultado coincide:
Por tanto, estas fracciones son equivalentes. Ahora veamos otro ejemplo:
Comprobemos si son equivalentes realizando las divisiones por separado:
Los cocientes son distintos, por lo que hemos comprobado que las fracciones no son equivalentes.
Por tanto, las fracciones equivalentes son aquellas que representan una misma relación entre el numerador y denominador. Además, toda fracción es proporcional a otra que sea equivalente, es decir, existe un número real que podemos multiplicar al numerador y denominador para obtener dicha fracción equivalente.
Cómo saber si dos fracciones son equivalentes
Una manera de saber si dos fracciones son equivalentes es la que hemos presentado anteriormente en el artículo: dividiendo los numeradores por sus denominadores. Si los resultados de la división coinciden, entonces son fracciones equivalentes.
Además, existen otras dos formas: mediante la multiplicación en X y mediante el mínimo común múltiplo.
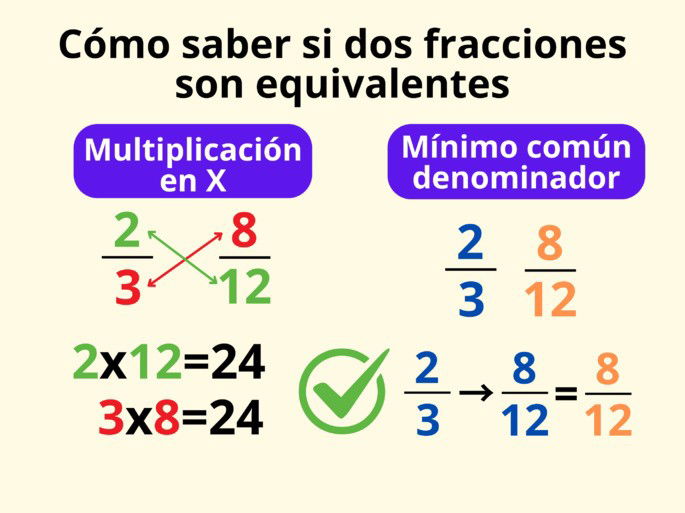
Por multiplicación en X
La multiplicación en X o en aspa es un método común para descubrir si dos fracciones son equivalentes. Para ello, basta con multiplicar el numerador de la primera fracción por el denominador de la segunda. A continuación, se multiplica el denominador de la primera fracción por el numerador de la segunda. Si los resultados coinciden, son fracciones equivalentes.
Veamos el siguiente ejemplo:
Hacemos la multiplicación en X y tenemos:
Los resultados coinciden; por tanto, acabamos de comprobar que estas dos fracciones son equivalentes.
Por mínimo común denominador
El objetivo del método del mínimo común denominador es el de ajustar las fracciones de forma que los denominadores coincidan. Luego, si vemos que los numeradores también son iguales, entonces son fracciones equivalentes. ¿Cómo hacemos eso?
Retomemos el ejemplo anterior. Primero, calculemos el mínimo común múltiplo de los denominadores:
Calculado el mínimo común múltiplo, ajustamos la primera fracción para que contenga el mismo denominador que la segunda fracción:
Como podemos ver, la fracción resultante tras ajustar la primera coincide con la segunda fracción. De esta forma, acabamos de demostrar que ambas fracciones son equivalentes.
Vea también Mínimo común múltiplo (mcm).
Cómo sacar fracciones equivalentes
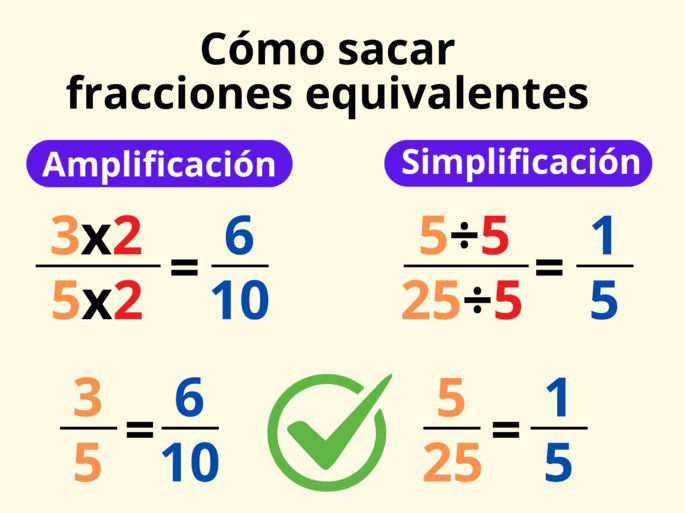
Existen dos métodos sencillos para encontrar fracciones equivalentes a partir de otra fracción: por amplificación y por simplificación. A continuación, explicamos estos métodos con un ejemplo.
Fracciones equivalentes por amplificación
El método de buscar fracciones equivalentes por amplificación se realiza multiplicando el numerador y denominador por un mismo número. Podemos obtener infinitas fracciones equivalentes mediante esta forma, pues hay infinitos números que sirven para multiplicar ambos términos.
Por ejemplo, si a la siguiente fracción multiplicamos el numerador y el denominador por 2 y por 3, obtendremos fracciones equivalentes:
Para comprobar que son equivalentes, dividimos los numeradores por sus denominadores, y vemos que el resultado es el mismo:
Fracciones equivalentes por simplificación
El método por simplificación es el proceso opuesto al de amplificación: en vez de multiplicar el numerador y denominador, dividimos ambos por un mismo número. A diferencia de la amplificación, no es habitual hallar más de dos o tres fracciones equivalentes usando esta forma.
Por ejemplo, si a la siguiente fracción dividimos los dos términos por 5, conseguiremos una fracción equivalente:
Para este método, conviene saber cuáles son los factores del numerador y el denominador, y anotar qué números coinciden. Cualquier número que sea un factor común entre el numerador y denominador, se puede utilizar para obtener una fracción equivalente mediante simplificación.
Por ejemplo, los factores de 5 y 25 son:
- Factores de 5: 1 y 5.
- Factores de 25: 1, 5 y 25.
Como 5 es un factor común, podemos dividir ambos términos por dicho número. Una forma de descubrir por cuál factor puedes dividir dos o más números es calculando el máximo común divisor.
Ejemplos de fracciones equivalentes con ejercicios resueltos
En esta sección compartimos una serie de ejercicios con solución sobre fracciones equivalentes para que puedas practicar por tu cuenta.
Ejercicio 1
Descubre si las siguientes fracciones son equivalentes o no:
Ejercicio 2
Comprueba si las siguientes fracciones son equivalentes o no:
Ejercicio 3
A partir de la siguiente fracción:
Saca dos fracciones equivalentes por amplificación.
Ejercicio 4
Tenemos la siguiente fracción:
Mediante el método de la simplificación, podemos sacar tres fracciones equivalentes. ¿Cuáles son?
Vea también:
Cómo citar: Rhoton, Stephen (05/05/2025). "Fracciones equivalentes". En: Significados.com. Disponible en: https://www.significados.com/fracciones-equivalentes/ Consultado: