Números racionales
Los números racionales son aquellos que se pueden representar como la división o fracción de dos números enteros. Si, por ejemplo, dividimos 30 entre 15, obtenemos 2, un número racional.
Q es el símbolo utilizado para englobar esta categoría de números. Para considerarse como número racional, la división a / b, en el que b es diferente de cero, ha de dar como resultado:
- Un número entero, como 6, -15 o 94.
- Una cifra con un número finito de decimales, como 1,575 o 0,24.
- Una cifra con un número infinito de decimales, pero que presenta una periodicidad o patrón repetido de decimales, como 0,888888...
Los números racionales son claves en las matemáticas, física, química y otras ciencias, así como en nuestro día a día. Son los números que utilizamos para cuantificar objetos y eventos, o entender la relación que existe entre dos cantidades diferentes.
Es importante tener presente que, para que un número sea racional, ha de ser resultado de la división de dos números enteros. Cuando no se puede hacer eso, decimos que es un número irracional.
Ejemplos de números racionales
Veamos unos cuantos ejemplos que ilustren cuáles son los números racionales, así como sus diferentes tipos.
Ejemplo de un número entero positivo
Los números enteros son uno de los tipos de números racionales, representados con el símbolo Z. Pongamos que tenemos el siguiente cociente:
Si realizamos la división o la simplificamos, vemos que da 5. Este es un número entero, ya que es un valor exacto sin decimales. Asimismo, es un número racional, pues hemos podido representar el 5 como el resultado de una división entre dos números enteros, 100 y 20.
Ejemplo de un número entero negativo
Los números racionales también pueden ser negativos. Veamos esta fracción:
En este caso, el cociente no resulta en una cifra positiva, sino negativa, menor de 0. Estos números se conocen como números enteros negativos, y también son parte de los números racionales.
Ejemplo de un número fraccionario con decimal exacto
Existen otros grupos de números que no forman parte de los enteros, pero siguen siendo racionales. Hablamos de los números fraccionarios con decimales.
Echemos un vistazo al siguiente ejemplo:
En esta ocasión, aunque el cociente se realice entre dos números enteros, la división no resulta en un número entero, sino fraccionario con decimal. Al haber solo dos cifras decimales, se conoce como número fraccionario con decimal exacto.
Toda cifra que contenga un número finito de decimales forma parte de los números racionales.
Ejemplo de un número fraccionario con decimal periódico
Sigamos con el ejemplo anterior, pero invirtiendo el numerador con el denominador:
Esta fracción devuelve un valor decimal periódico. En este caso, quiere decir que el número decimal 3 se repite indefinidamente. Aunque tenga un número infinito de decimales, sigue siendo un número racional, ya que es resultado de la división entre dos números enteros.
Este tipo de números se clasifica como números fraccionarios con decimal periódico.
Ejemplo de un número irracional
Ahora veamos un ejemplo de un número que no es racional, es decir, es irracional. El número pi (π), por ejemplo, se utiliza mucho en matemáticas y física:
Aunque es común utilizar la aproximación 3,14, pi es un valor que contiene infinitas cifras decimales no periódicas. A raíz de esto, no se puede representar como el cociente de dos números enteros a y b. Por ello, no puede ser un número racional, sino que es irracional.
Clasificación de los números racionales
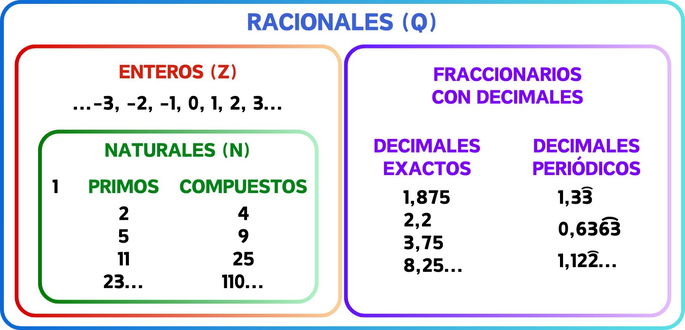
Los números racionales se dividen en diferentes tipos según las características que tengan, y se clasifican de la siguiente forma:
-
Números enteros (Z), que son aquellos números sin decimales, divididos en:
- El 0.
- Los enteros negativos.
- Los números naturales (N).
- 1.
- Los números naturales primos.
- Los números naturales compuestos.
-
Fraccionarios con decimales.
- Cifras con decimales exactos.
- Cifras con decimales periódicos.
- Periódicos puros, con toda la parte decimal repitiéndose indefinidamente.
- Periódicos mixtos, con una parte de las cifras decimales que no se repite.
Vea también Números enteros, Números naturales y Números primos.
Características y propiedades de los números racionales
Los números racionales nos indican la relación que existe entre dos números enteros a y b. Asimismo, cada número racional puede representarse como una combinación infinita de numeradores y denominadores, siempre que se mantenga la misma relación.
Entre dos números racionales cualesquier hay infinitos números racionales e irracionales. Por ejemplo, entre el 1 y 2 hay números racionales como 1,2 o 1,745. No obstante, la raíz cuadrada de 2, de valor aproximado 1,41, es en realidad un número irracional, con una cantidad indefinida de decimales no conocidos.
Por último, sumar, restar, multiplicar o dividir dos números racionales siempre resulta en otro número racional. Ahora, aplicar la raíz a un número, como por ejemplo la raíz cuadrada o cúbica, puede devolver un número racional o irracional.
Diferencia entre números racionales e irracionales
Los números irracionales son aquellos que no se pueden representar como el cociente de dos números enteros a y b. Este grupo engloba aquellos números que contienen una cantidad de cifras decimales no repetidos.
Por lo tanto, los números racionales con cantidad infinita de decimales se distinguen por tener una periodicidad o seguir un patrón. Es decir, siempre que haya una cifra o grupo de cifras conocidos que se repite continuamente. No es así con los números irracionales.
Vea también:
Cómo citar: (11/12/2023). "Números racionales". En: Significados.com. Disponible en: https://www.significados.com/numeros-racionales/ Consultado: