Qué es un Polígono
Un polígono es una figura geométrica cerrada y plana que está formada por varios segmentos rectos unidos, también denominados lados.
Los puntos donde empiezan y terminan cada uno de los segmentos o lados se llaman vértices, y el polígono tendrá el mismo número de vértices que de lados.
Por ejemplo, un hexágono es un polígono que tiene seis lados y seis vértices. El pentágono tiene cinco lados y cinco vértices.
Generalmente, los polígonos reciben sus respectivos nombres en función del número de lados que poseen, aquí ofrecemos varios ejemplos:

Triángulo: polígono de tres lados.
Cuadrilátero: polígono de cuatro lados.
Paralelogramo: polígono de cuatro lados cuyos lados opuestos son paralelos.
Rombo: polígono de cuatro lados con lados y ángulos opuestos iguales.
Cuadrado: polígono de cuatro lados iguales y cuatro ángulos rectos.
Rectángulo: polígono de cuatro lados, con lados opuestos iguales y ángulos rectos.
Romboide: polígono de cuatro lados con lados opuestos iguales y paralelos.
Trapezoide: polígono de cuatro lados, sin lados paralelos.
Trapecio: polígono de cuatro lados, con dos lados paralelos y dos no paralelos.
Pentágono: polígono de cinco lados y cinco ángulos.
Hexágono: polígono de seis lados y seis ángulos.
Heptágono: polígono de siete lados y siete ángulos.
Octágono: polígono de ocho lados y ocho ángulos.
Eneágono: polígono de nueve lados y nueve ángulos.
Decágono: polígono de diez lados y diez ángulos.
Endecágono: polígono de once lados y once ángulos.
Dodecágono: polígono de doce lados y doce ángulos.
Estrellado: polígono de un número determinado de lados, que se extienden hacia afuera, formando puntas o ramas.
Elementos del polígono
Los polígonos constan de diferentes elementos:
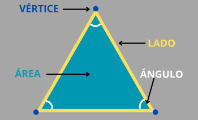
- Lados: son cada uno de los segmentos que conforman el polígono y están unidos por los vértices.
- Vértices: son puntos de unión que representan los extremos de cada segmento.
- Ángulos: se forman cuando dos lados de un polígono concurren en un mismo vértice.
- Ángulo interior: se encuentra dentro del polígono.
- Ángulo exterior: es el que queda fuera del polígono.
- Diagonales: que son segmentos que unen dos vértices no consecutivos.
- Apotema: es un segmento que va desde el centro del polígono hasta la mitad de uno de sus lados.
- Centro del polígono: es el punto que se encuentra a la misma distancia de todos sus vértices.
- Área de un polígono: es la superficie que se encuentra dentro de la línea poligonal, está demarcada por el perímetro.
- Perímetro de un polígono: es la suma de la longitud de todos sus lados.
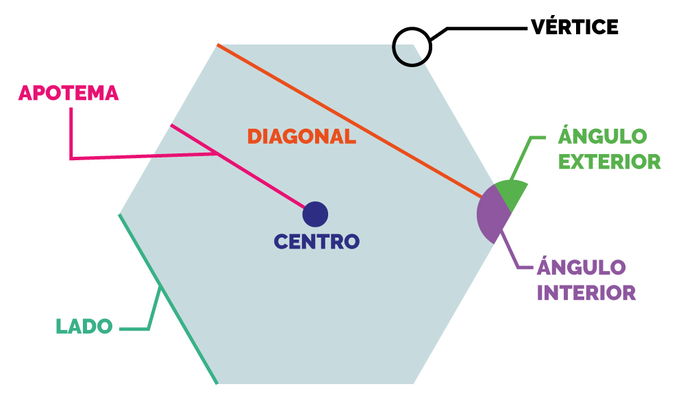
Todos estos elementos son comunes en todos los tipos de polígonos, excepto la apotema y el centro, que solo los encontraremos en polígonos regulares.
Cómo calcular los ángulos de un polígono
Para calcular los ángulos interiores de un polígono hemos de seguir la siguiente fórmula , donde n representa el número de lados del polígono. Si, por ejemplo, queremos calcular la medida total de los ángulos internos de un cuadrado, calcularemos:
360º es la suma de los 4 ángulos internos de un cuadrado.
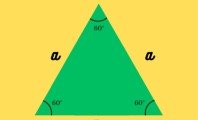
Para calcular la medida de cada uno de los ángulos internos de un polígono regular, utilizaremos la misma fórmula y dividiremos el resultado entre n. Tomemos como ejemplo un hexágono.
Es decir, cada ángulo interno en un hexágono regular medirá 120º.
Los ángulos externos de cualquier polígono suman un total de 360º, por tanto, para calcular la medida de cada ángulo únicamente hay que dividir entre n. Si tomamos como ejemplo el hexágono dividiremos:
Es decir, cada ángulo externo medirá 60º.
Cabe aclarar que los ángulos internos y externos son suplementarios, es decir, la suma de ambos ángulos debe dar 180º. Por tanto, si un ángulo externo de un hexágono mide 60º, el interno medirá 120º.
Cómo calcular el perímetro y el área de un polígono
El perímetro se alcanza sumando la medida de todos los lados, si el polígono es regular podemos multiplicar el número de lados por la medida de uno de lados (P = n·l).
La forma de calcular el área de un polígono varía en función de si este es regular o irregular. En el caso de los polígonos regulares, el área se calcula multiplicando el valor del perímetro por el valor de la apotema y el resultado se divide entre dos:
.
El área de un triángulo se multiplica la base por la altura y se divide entre 2:
El área de un cuadrado se halla multiplicando lado por lado (A = l · l). La del rectángulo se calcula multiplicando el lado mayor por el lado menor (A= L · l).
Para realizar este cálculo en determinados polígonos irregulares, hay que simplificar la figura en otras más sencillas. Por ejemplo, la estrella de seis puntas puede descomponerse en dos triángulos. Calculando y sumando el área de ambos triángulos hallaríamos el área del polígono estrellado.
Ver también Perímetro, Figuras geométricas y Cuerpos geométricos.
Tipos de polígonos

Polígono regular e irregular
El polígono regular se caracteriza porque sus lados tienen la misma longitud, sus ángulos interiores son de la misma medida y sus vértices se encuentran circunscritos en una circunferencia. Son polígonos equiláteros y equiangulares, ya que todos sus lados y todos sus ángulos miden lo mismo.
En cambio, el polígono irregular se distingue porque sus lados no tienen la misma longitud, sus ángulos interiores no son de la misma media y sus vértices no quedan suscritos en una circunferencia.
También puede ver Polígonos regulares y Polígonos Irregulares.
Polígono convexo y cóncavo
El polígono convexo es aquel cuyos ángulos interiores miden menos de 180°, o π (3,14) radianes, y sus diagonales son siempre interiores.
El polígono cóncavo, en cambio, posee ángulos interiores que miden más de 180°, o π radianes, y una de sus diagonales es exterior al polígono.
Puede ver más en Polígono Convexo.
Polígono inscrito y circunscrito
El polígono inscrito es el que está dentro de otra figura geométrica, generalmente una circunferencia. Es decir, todos los lados del polígono están encuadrados dentro de la otra figura.
El polígono circunscrito es lo contrario del anterior, ya que el polígono contiene en su interior otra figura geométrica.
Polígono simple y complejo
El polígono simple es aquel cuyas aristas no se cruzan entre sí, por tanto, no se cortan a sí mismos, no hay intersecciones entre sus lados. Un cuadrado, por ejemplo, es un polígono simple.
Polígonos complejos o cruzados, son aquellos en los que existen intersecciones entre sus lados, es decir, sus lados se cruzan en algún punto. Pueden estar formados por varios polígonos simples que comparten un lado o vértice común.
Un ejemplo de polígono complejo sería un polígono estrellado de seis puntas, integrado por dos triángulos superpuestos.
Vea también:
Referencias bibliográficas:
-
Godino, J. D., & Ruíz, F. (2002). Geometría y su didáctica para maestros. Universidad de Granada, Departamento de Didáctica de la Matemática.
Cómo citar: Significados, Equipo (20/11/2024). "Qué es un Polígono". En: Significados.com. Disponible en: https://www.significados.com/poligono/ Consultado: