Triángulo equilátero
Qué es un Triángulo Equilátero:
Un triángulo equilátero es aquel cuyos lados tienen la misma longitud y cuyos ángulos internos presentan la misma medida. Esta es la propiedad fundamental para poder definir un triángulo como equilátero y lo que hace que forme parte de los polígonos regulares.
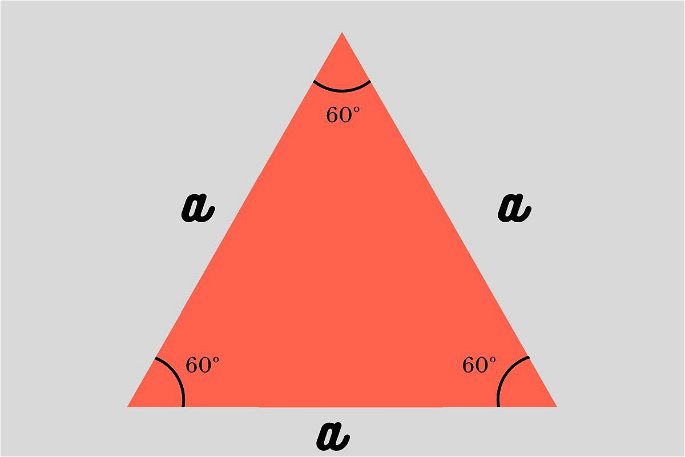
Triángulo equilátero: lados y ángulos internos.
Pero los triángulos equiláteros presentan otras propiedades y características más:
Además de tener tres lados que miden exactamente lo mismo, el triángulo equilátero posee tres ángulos internos que también son iguales, es decir, son congruentes.
Recordemos que la suma total de los ángulos internos de un triángulo es 180º, por lo que la medida de cada ángulo interno en este caso es de 60º.
Cada uno de los ángulos externos de un triángulo equilátero mide 120º, que sumados a la medida del ángulo interno (60º) da como resultado los 180º. Es decir, los ángulos internos y externos de un triángulo equilátero son suplementarios.
El centro de simetría de un triángulo equilátero es el punto donde se encuentran sus medianas. Las medianas son los segmentos que unen cada uno de sus vértices con el medio del lado opuesto. En el triángulo equilátero, las medianas coinciden con la altura del triángulo.
Además, todos los vértices del triángulo equilátero están situados a la misma distancia del centro del polígono. Es decir, si trazamos una circunferencia desde dicho centro, esta pasará por cada uno de los vértices del triángulo. El triángulo equilátero, como sucede con otros polígonos regulares, está circunscrito a una circunferencia.
Fórmulas del triángulo equilátero y ejemplos
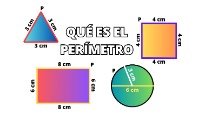
Perímetro
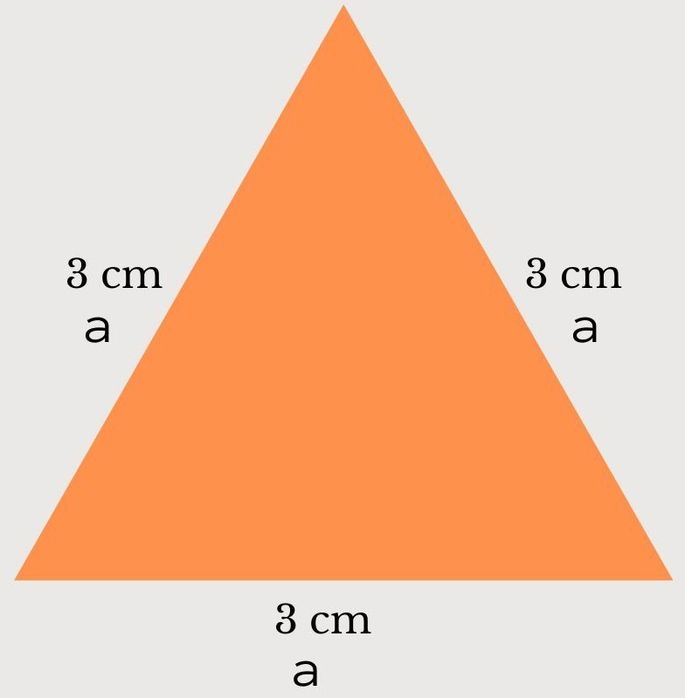
Para calcular el perímetro de un triángulo equilátero debemos sumar todos sus lados, o lo que es lo mismo, multiplicar por tres la medida de uno de los lados.
Por ejemplo, el perímetro del triángulo de la imagen, cuyos lados miden 3 cm, será de 9 cm:
Altura
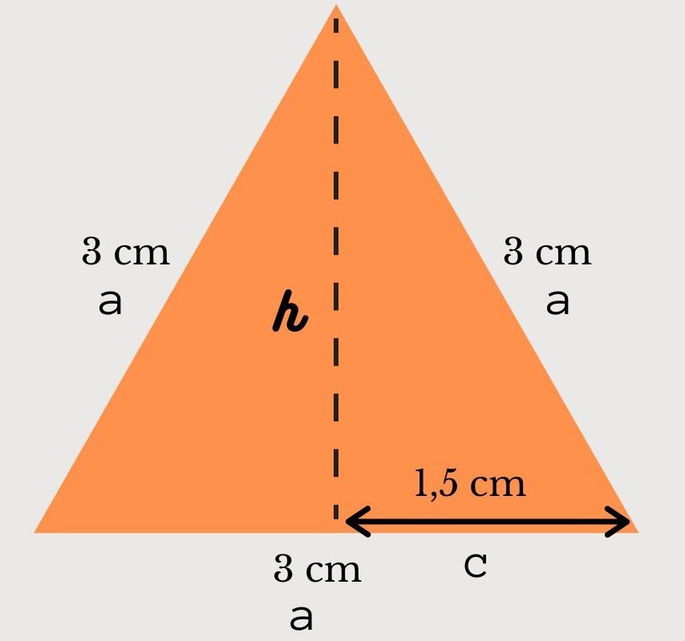
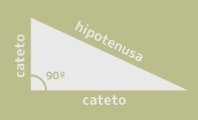
La altura es el segmento que va desde el vértice superior hasta la mitad de la base, dividiendo el triángulo en dos triángulos rectángulos.
Como únicamente conocemos la medida de los lados del triángulo, y aprovechando los triángulos rectángulos resultantes, vamos a utilizar el Teorema de Pitágoras para calcular el valor de la altura.
El Teorema de Pitágoras dice que:
“En un triángulo rectángulo, la hipotenusa al cuadrado es igual a la suma de los dos catetos al cuadrado”
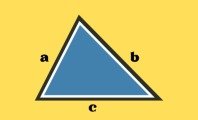
Nosotros conocemos el valor de a, que es 3 cm, y el valor de c, que es 1,5 cm. Nos faltaría conocer el valor de h (altura). Por lo que:
Por tanto, ahora ya sabemos que la altura de nuestro triángulo es de 2,5 cm.
Ver también Teorema de Pitágoras
Área

Ahora podemos calcular el área del triángulo equilátero. Para conocer el área de cualquier triángulo debemos realizar el cálculo basándonos en la siguiente fórmula, donde A es el área, b es la base y h es la altura.
Por ejemplo, vamos a calcular el área del triángulo que mostramos en la imagen.
Ver también:
Cómo citar: (20/07/2023). "Triángulo equilátero". En: Significados.com. Disponible en: https://www.significados.com/triangulo-equilatero/ Consultado: