Polígonos Regulares
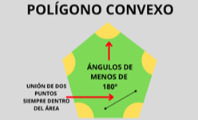
Los polígonos regulares son aquellos cuyos lados y ángulos miden lo mismo. Estas figuras geométricas, planas y cerradas, están formadas por un número determinado de segmentos, iguales entre sí, que se unen mediante sus extremos o vértices.
Todos los vértices de un polígono regular están situados a la misma distancia del centro del polígono y todos sus ángulos (internos, externos y centrales) presentan la misma medida.
Por ejemplo, un cuadrado es un polígono regular porque sus cuatro lados, unidos por cuatro vértices, son iguales y todos sus ángulos, internos y externos, miden 90º.
Los polígonos regulares, además, poseen un centro simétrico, que cumple dos funciones: es el vértice para los ángulos centrales y también el extremo de la apotema, que es el segmento que une el centro de un polígono con la mitad de uno de sus lados.
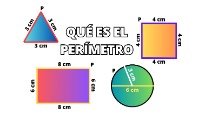
La apotema es un elemento imprescindible a la hora de calcular el área del polígono regular, de la misma forma que el perímetro, que es la suma de todos los lados del polígono.
Para calcular el área se multiplica el perímetro por la apotema y se divide entre dos, tal como se muestra en la siguiente fórmula:
Otra de las particularidades de este tipo de polígonos es que sus diagonales son todas de la misma longitud, es decir, que la distancia entre vértices no consecutivos es la misma. Únicamente el triángulo no comparte este rasgo porque solamente tiene tres vértices.
Cada polígono tiene un número determinado de diagonales que varía en función del número de vértices. La fórmula para calcular las diagonales de un polígono es multiplicar el número de lados por dicho número menos tres y dividir ese resultado entre dos:
Por ejemplo, si deseamos saber el número de diagonales de un octógono, polígono de ocho lados (n = 8), la operación sería esta:
Por tanto, un octógono tiene 20 diagonales.
Clasificación de los polígonos regulares
Un polígono regular puede tener un número infinito de lados, por lo que en esta clasificación presentamos algunos de los más habituales.
Triángulo equilátero

Polígono regular de 3 lados iguales, cada uno de sus ángulos internos miden 60°. No dispone de diagonales porque al tener solo tres vértices siempre son consecutivos. Su perímetro es el resultado de multiplicar por tres la medida del lado (P= 3·L)
La fórmula para calcular el área de un triángulo equilátero es multiplicar base por altura y dividir entre dos:
Cuadrado

Tiene 4 lados iguales, cada ángulo interno mide 90°, consta de dos diagonales. La fórmula para hallar su perímetro es multiplicar por cuatro la longitud del lado (P = 4·L)
Su área se calcula multiplicando lado por lado (A = l·l) o elevar el valor del lado al cuadrado.
Ver también Cuadrado
Pentágono regular

Figura de 5 lados iguales, cada ángulo interno mide 108°. El pentágono posee cinco diagonales y su perímetro se calcula multiplicando por cinco la medida de uno de sus lados (P = 5·L). La fórmula para calcular su área es:
Hexágono regular

Polígono de 6 lados iguales, cada ángulo interno mide 120°. Un hexágono consta de 9 diagonales, la fórmula para calcular su perímetro es P = 6·L y la fórmula para calcular su área:
Heptágono regular

Consta de 7 lados iguales, cada ángulo interno mide 128,57°, tiene 14 diagonales, su perímetro se calcula multiplicando por siete la longitud del lado P = 7·L y la fórmula para calcular su área
Octógono regular

Posee 8 lados iguales, cada ángulo interno mide 135°, consta de 20 diagonales, su perímetro se halla mediante P = 8·L y su área
Eneágono regular

También llamado nonágono, está formado por 9 lados iguales, cada ángulo interno mide 140°. Posee 27 diagonales, su perímetro se calcula multiplicando por nueve la medida del lado P = 9·L y su área:
Decágono regular

Es un polígono de 10 lados iguales, cada ángulo interno mide 144°. Tiene 35 diagonales, su perímetro se halla mediante P = 10·L y su área
Endecágono regular

Presenta 11 lados iguales, cada ángulo interno mide 147,27°. Consta de 44 diagonales, la fórmula para hallar el perímetro es P = 11·L y para el área
Dodecágono regular

Un dodecágono está formado por 12 lados iguales, cada ángulo interno mide 150°. Integra 54 diagonales, la fórmula para encontrar su perímetro es P = 12·L y para hallar el área:
Icoságono regular

Tiene 20 lados iguales, cada ángulo interno mide 162º. Consta de 170 diagonales, su perímetro se calcula mediante P = 20·L y su área con:
Triacontágono regular

Formado por 30 lados iguales, cada ángulo interno mide 168º. Presenta 405 diagonales, la fórmula que calcula su perímetro es P = 30·L y el área
Tetracontágono regular

Tiene 40 lados iguales, cada ángulo interno mide 171º y tiene 740 diagonales. El perímetro se halla calculando P = 40·L y el área
Pentacontágono regular

Polígono de 50 lados iguales, cada ángulo interno mide 172.8º. Su número de diagonales es 1175, podemos encontrar su perímetro con esta fórmula P = 50·L y el área con:
Características y elementos de los polígonos regulares
Sus lados y ángulos internos son iguales
Los polígonos regulares están compuestos por un número finito de lados y todos miden lo mismo. Sus ángulos internos también tienen la misma medida. Esta característica les otorga una gran simetría y regularidad que los diferencia de otros polígonos.
Los polígonos regulares también poseen ángulos centrales, es decir, ángulos que tienen su vértice en el centro del polígono. Todos los ángulos centrales también poseen la misma medida.
Poseen un centro de simetría
Cada polígono regular tiene un centro de simetría, que es el punto donde se cortan todas sus diagonales. Este punto es también el centro de un círculo circunscrito que pasa por todos los vértices del polígono.
Diagonales
Las diagonales son segmentos que unen vértices no consecutivos del polígono. En función del número de lados y, por tanto, del número de vértices, variará el número de diagonales.
Para calcular cuántas diagonales tiene un polígono debemos multiplicar el número de lados (n) por el resultado de restar a dicho número el 3, es decir, n·(n-3) y lo dividiremos entre dos.
.
Si por ejemplo queremos saber cuántas diagonales tiene un pentágono regular (polígono de 5 lados y 5 vértices) haremos la siguiente operación:
También podemos calcular el número de diagonales que nacen da cada vértice de forma sencilla con la siguiente fórmula (d=n-3), es decir, restando el número 3 al número de lados del polígono.
Se resta el número 3 porque no se cuenta el vértice del que partimos ni los dos vértices consecutivos.
Área y perímetro
El área de un polígono regular se puede calcular fácilmente si conocemos la longitud de su apotema y su perímetro. La apotema es la distancia que hay desde el centro del polígono hasta el centro de uno de sus lados. El perímetro es la suma de la longitud de todos sus lados.
La fórmula para calcular el área de un polígono regular es el perímetro multiplicado por la apotema dividido entre dos:
Ver también:
Referencias:
Quintero, A. H., & Costas, N. (1994). Geometría. La Editorial, UPR.
Cómo citar: (21/04/2023). "Polígonos Regulares". En: Significados.com. Disponible en: https://www.significados.com/poligonos-regulares/ Consultado: