Radicación
La radicación es una operación matemática que consiste en encontrar la raíz de un número. Es la operación inversa de la potenciación, pues la radicación de un número busca hallar aquella cifra que, multiplicada por sí misma un número de veces, dé dicho número.
Por ejemplo, ¿por qué la raíz de 4, es decir, √4, es 2? Si realizamos la potenciación de 2 al cuadrado, 22, vemos que nos da 4. Por tanto, la raíz cuadrada de 4 es 2.
Otra forma de definir la radicación es que resulta de elevar a un número un exponente fraccionario de valor entre 0 y 1. Por ejemplo, la raíz cuadrada de 5, √5, es igual a 51/2. De igual manera, la raíz cúbica de 8, 3√8, se puede representar como 81/3.
La radicación contiene las siguientes partes: el símbolo de la radicación, el radicando, el índice y la raíz.
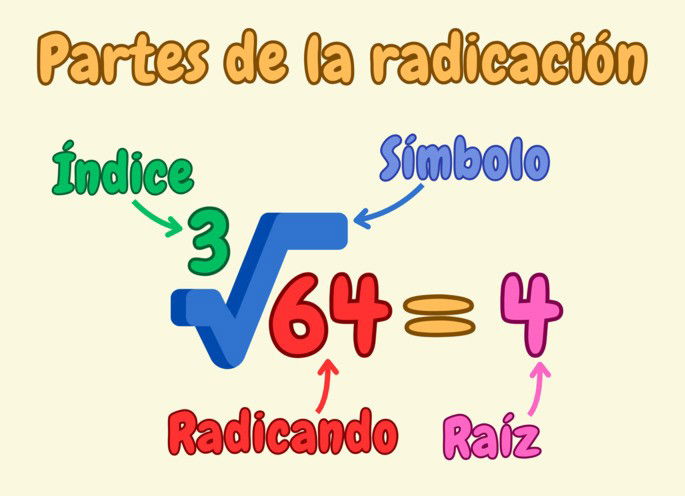
Símbolo de la radicación: representado con el símbolo √, nos muestra que estamos ante una operación de radicación. Contiene el radicando.
Radicando: es aquel número cuya raíz deseamos hallar. Se ubica dentro del símbolo de la radicación, y ha de ser siempre un número real positivo cuando el índice de la raíz es par.
Índice de la raíz: es el número que indica el orden de la raíz, y ha de ser siempre un número natural. Por ejemplo, si es 2 (2√ o √), se trata de una raíz cuadrada; si es 3 (3√), se trata de una raíz cúbica; etc.
A su vez, el índice es también el número al que debemos elevar a la raíz para que nos dé el radicando. Por ejemplo, sabemos que 3√125 = 5, pues 53 = 125.
Además, el índice de la raíz coincide con el denominador del exponente del radicando. Por ejemplo:
Raíz: es el número que resulta de la operación de radicación. Este número, al elevarlo por el índice de la raíz, devuelve la misma cifra que el radicando.
Para ilustrar los términos que componen la radicación, veamos el siguiente radical:
En el que:
- 8 es el radicando;
- 3 es el índice, el cual nos indica que es una raíz cúbica;
- y 2 es la raíz, ya que 23 = 8.
Propiedades de la radicación
La radicación presenta una serie de propiedades, algunas con relación a la naturaleza de los radicales y otras que nos permiten simplificar o resolver una operación de diferentes formas.
Raíces positivas y negativas
Un radical de índice par (2√, 4√, 6√, etc.) y con radicando real positivo da como resultado dos raíces de la misma magnitud y signo diferente. No obstante, se acostumbra a dar solamente el valor absoluto de la raíz.
Por ejemplo, la raíz cuadrada de cuatro (√4) es 2 y -2, pues:
- 22 = 4
- (-2)2 = 4
En los radicales de índice par, si el radicando es negativo, la raíz siempre es un número complejo.
Ahora, si un radical es de índice impar (3√, 5√, 7√, etc.), el radicando puede ser un número real positivo o negativo, y el resultado siempre será una raíz real del mismo signo.
Veamos dos ejemplos:
- 3√27 = 3, pues 33 = 27
- 3√-27 = -3, pues (-3)3 = -27
Raíz de un producto
Una propiedad es la raíz de un producto de dos variables distintas, en la que se cumple la siguiente igualdad:
Por ejemplo, si tenemos la raíz de 9 · 16, entonces:
Raíz de un cociente
Otra propiedad de la radicación es la raíz de un cociente, en el que:
Por ejemplo, la raíz del cociente 9 / 16 es:
Raíz de una potencia
Cuando el radicando está elevado a una potencia, se cumple la siguiente relación:
Por ejemplo, si queremos hallar la raíz cuadrada de 34, podemos resolver de la siguiente forma:
Podemos aprovechar esta propiedad para simplificar la radicación de la siguiente forma: si la potencia coincide con el índice del radical, ambos se anulan. Por ejemplo:
Raíz de una raíz
Cuando deseamos calcular la raíz de una raíz, podemos multiplicar los índices de ambas raíces. Es decir:
Vea el siguiente ejemplo:
Producto de radicales con índices diferentes y mismo radicando
Cuando se multiplican dos radicales cuyo radicando coinciden, pero presentan distintos índices, se cumple la siguiente igualdad:
Por ejemplo:
Raíz de 0 y 1
En la radicación hay un caso particular a tener en cuenta: cuando el radicando es 0 o 1. Como 0 multiplicado por sí mismo es igual a 0, ello implica que la raíz de 0 siempre será 0, sin importar el índice del radical. Lo mismo sucede con 1; aunque se multiplique por sí mismo docenas y centenas de veces, el resultado siempre será 1.
Por tanto, la última propiedad a destacar es:
Ejemplos de radicación
Aquí compartimos cuatro ejercicios de radicación que te servirán para practicar y aprender más sobre las propiedades de la radicación.
Ejemplo 1
Resuelve las siguientes radicaciones:
Ejemplo 2
Resuelve las siguientes radicaciones sirviéndote de las propiedades:
Ejemplo 3
¿Cuáles de las siguientes radicaciones se pueden simplificar?
Ejemplo 4
¿Cuál es la respuesta correcta de la siguiente radicación?
a) 5
b) 16
c) 8
Vea también:
Cómo citar: Significados, Equipo (04/06/2025). "Radicación". En: Significados.com. Disponible en: https://www.significados.com/radicacion/ Consultado: