Área de un círculo
El área de un círculo es el espacio comprendido en su interior, delimitado por una línea curva llamada circunferencia. Imaginemos, por ejemplo, una moneda. El área sería la superficie que está en el interior de la circunferencia que delimita dicha moneda.
Antes de calcular el área de un círculo, tenemos que conocer dos elementos:
- El número pi, representado por el símbolo π. Este número equivale a una cantidad aproximada de 3,14159.
- El radio (r) del círculo. El radio es la distancia en línea recta desde el centro del círculo hasta el perímetro o circunferencia, que es la línea curva exterior que le da forma.
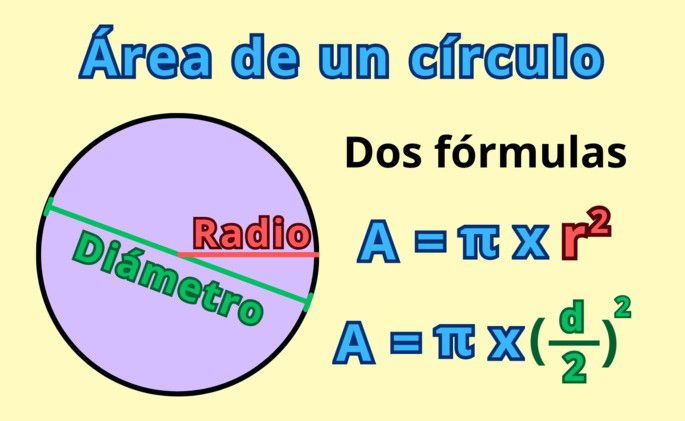
Una vez que tenemos estos dos elementos, pasamos al cálculo. El área de un círculo se calcula mediante la siguiente fórmula:
A = π x r2
Es decir, el área (A) es el resultado de multiplicar el número pi (π) por el radio (r) al cuadrado. El número resultante se representa en milímetros, centímetros, metros, etc., cuadrados.
Por ejemplo, si tenemos un círculo cuyo radio es de 10 cm, el área es A = 3,14159 x 102 = 314,159 cm2.
En ocasiones, sabremos el valor del diámetro del círculo, en vez de su radio. Recuerda que la relación entre el diámetro y el radio es que el radio es la mitad del diámetro. Es decir: r = d/2.
Por tanto, otra forma de escribir la fórmula del área del círculo es A = π x (d/2)2. Para ilustrar con un ejemplo, imaginemos que del círculo anterior conocemos su diámetro, de 20 cm, en vez de su radio.
En este caso, aplicamos la fórmula alternativa: A = π x (d/2)2 = π x (20/2)2 = π x 102 = 314,159 cm2.
Ejemplos del cálculo del área de un círculo
Ejemplo 1
Imaginemos que un círculo posee un radio de 15 centímetros. ¿Cuál es su área?
Ejemplo 2
Se nos presenta un círculo cuyo radio tiene 27 centímetros de longitud. En este caso, ¿cuál es el área del círculo?
Ejemplo 3
Un círculo determinado posee un diámetro de 63 centímetros de longitud. ¿Qué área tiene este círculo?
Ejemplo 4
El tercio del diámetro de un círculo es de 8 centímetros de longitud. ¿Qué área tiene este círculo?
Área y perímetro de un círculo
El área y el perímetro de un círculo son conceptos diferentes que a veces se confunden. A continuación, pasamos a diferenciarlos.
El perímetro es la longitud de la línea curva que forma el círculo. Dicho de otro modo, es la longitud del borde del círculo. Para calcular su longitud, se multiplica el diámetro (el diámetro es doble que el radio) por el número pi (π), es decir, P = d x π.
El área, en cambio, es toda la superficie encerrada dentro del perímetro. Se mide en unidades cuadradas y se calcula multiplicando el número pi (π) por el radio al cuadrado. Por tanto, el valor del área de un círculo siempre será mayor que el de su perímetro.
Vea también:
Cómo citar: Rhoton, Stephen (04/09/2025). "Área de un círculo". En: Significados.com. Disponible en: https://www.significados.com/area-de-un-circulo/ Consultado: