Diámetro
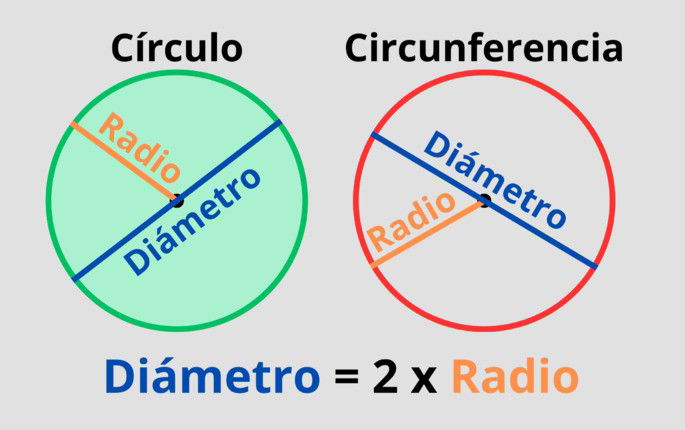
El diámetro es la recta que cruza el centro de un círculo, uniendo dos puntos de su perímetro. Este segmento también define el ancho de un círculo, circunferencia, semicírculo o esfera.
El símbolo del diámetro puede ser D, d o Ø. Sus unidades dependerán del tamaño del círculo, pero suelen emplearse el milímetro, centímetro, metro o kilómetro.
La palabra diámetro tiene raíces griegas. Está compuesta por el prefijo dia- que significa a través y la palabra metron que se refiere a la medida.
Podemos calcular el diámetro de cualquier círculo si tenemos en nuestra mano una regla o cinta métrica. Basta con comenzar en el perímetro de la figura y leer la distancia que se recorre hasta el punto opuesto. ¡Asegúrate de que la regla o cinta métrica pase por el centro del círculo!
Algunos ejemplos de diámetro de objetos esféricos son:
- Pelota de béisbol: tiene un diámetro entre 7,3 y 7,5 centímetros.
- Pelota de fútbol: tiene un diámetro aproximado de 22 centímetros.
- Pelota de baloncesto: tiene un diámetro aproximado de 24 centímetros.
- La Tierra: tiene un diámetro aproximado de 12,742 kilómetros.
- La luna: tiene un diámetro aproximado de 3,474 kilómetros.
- El sol: tiene un diámetro aproximado de 1,3914 millones de kilómetros.
Fórmula para sacar el diámetro
En geometría, el diámetro de un círculo se calcula mediante diversas fórmulas, según los datos que conozcamos. La fórmula más conocida es aquella que relaciona el diámetro con el radio del círculo o circunferencia.
En este sentido, la fórmula es:
D = 2r
En el que D es el diámetro del círculo o circunferencia, y r su radio. El radio es una recta que une el centro del círculo con un punto del perímetro, por lo que es igual a la mitad del diámetro. O lo que es lo mismo, el diámetro es el doble del radio.
Otras fórmulas para calcular el diámetro
Además de la fórmula presentada anteriormente, el diámetro se puede calcular a partir del perímetro o circunferencia de un círculo. La fórmula es:
En el que P es el perímetro, y π corresponde al número pi, de un valor aproximado de 3,141592. Por tanto, siempre que conozcamos el perímetro o la longitud de la circunferencia, seremos capaces de calcular el diámetro.
La otra fórmula que podemos emplear es aquella que relaciona el diámetro con el área de un círculo:
En el que A se refiere al área. De esta forma, verás que a partir del área podemos calcular tanto el diámetro como el radio de un círculo (mediante la ecuación A = π x r2).
Vea también Círculo y Perímetro.
Ejemplos del cálculo de diámetro
Los siguientes ejercicios a modo de ejemplo te servirán para asimilar los conocimientos sobre el diámetro.
Ejercicio 1
Si tres esferas presentan un radio de 65, 72 y 89 centímetros, respectivamente, ¿cuáles son sus diámetros?
Ejercicio 2
Imagina un círculo cuyo radio desconocemos, pero sí sabemos que tiene un perímetro de 31,416 centímetros. Responde:
a) ¿Es posible calcular el diámetro del círculo?
b) Si es así, ¿cuál es el valor del diámetro?
Ejercicio 3
El único dato que conocemos de un círculo es que posee un área de 125 metros cuadrados. ¿Cuál es la longitud de su diámetro?
Vea también Símbolo pi (π).
Cómo citar: Rhoton, Stephen (21/05/2025). "Diámetro". En: Significados.com. Disponible en: https://www.significados.com/diametro/ Consultado:
