Razones trigonométricas
Las razones trigonométricas son relaciones entre los lados de un triángulo rectángulo que determinan sus ángulos. Este concepto está relacionado con operaciones matemáticas como el seno, coseno y tangente.
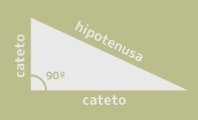
Los lados de un triángulo rectángulo están compuestos por dos catetos, o lados, y una hipotenusa. A su vez, los ángulos que describen este triángulo suman 180º en total, siendo uno de ellos 90º (llamado ángulo recto). Los otros dos ángulos son agudos, o sea menores de 90º, y podemos calcularlos a partir de las razones trigonométricas.
Las 6 razones trigonométricas y sus fórmulas
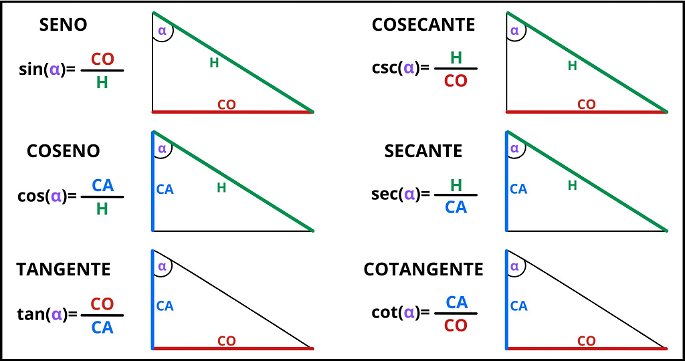
Las seis razones trigonométricas en un triángulo rectángulo son: seno, coseno, tangente, secante, cosecante y cotangente. Veamos una por una cómo se calculan estas razones y qué relación hay entre ellas, tomando como referencia un ángulo alfa (α).
Seno
El seno de un ángulo es la relación entre el cateto opuesto y la hipotenusa. Para ayudarnos a recordar esto, podemos memorizar las siglas SOH, que indican que el Seno es el Opuesto sobre Hipotenusa.
El seno se abrevia comúnmente como sin, o a veces como sen. Es también la inversa del cosecante, o la división entre coseno y cotangente:
Coseno
El coseno de un ángulo es la relación entre el cateto adyacente y la hipotenusa. Es decir, el Coseno es el Adyacente sobre Hipotenusa, o CAH:
El coseno se abrevia como cos, y es también la inversa del secante, o la división entre seno y tangente:
Tangente
La tangente de un ángulo es la relación entre el cateto opuesto y el adyacente. O sea, la Tangente es el Opuesto sobre Adyacente, o TOA:
La tangente se abrevia como tan o tg, y es también la inversa de la cotangente, o la división entre el seno y coseno:
Cosecante
La cosecante de un ángulo es la relación entre la hipotenusa y el cateto opuesto:
Es la inversa del seno, y se abrevia como csc o cosec. Otra forma de calcular esta razón es dividiendo la cotangente del ángulo por el coseno:
Secante
La secante de un ángulo es la relación entre la hipotenusa y el cateto adyacente:
Es la inversa del coseno, y se abrevia como sec. También podemos calcular esta razón mediante la división entre la tangente y el seno:
Cotangente
Finalmente, la cotangente de un ángulo es la relación entre el cateto adyacente y el opuesto:
La cotangente es la operación inversa de la tangente, y se abrevia como cot o ctg. Otra manera de calcularla es con la división entre coseno y seno:
Vea también Triángulo rectángulo e Hipotenusa.
Ejemplos de cálculos usando razones trigonométricas
Cálculo de los ángulos α y β usando el seno y la tangente
Imaginemos que tenemos el siguiente triángulo rectángulo:
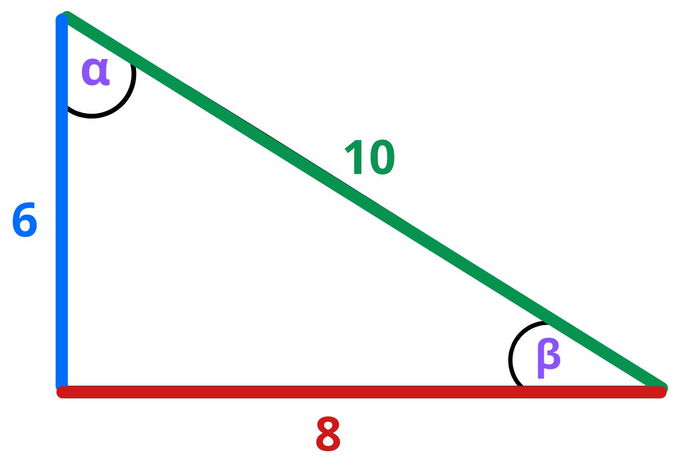
Los valores que conocemos son:
- Cateto vertical: 6
- Cateto horizontal: 8
- Hipotenusa: 10
- Ángulo recto: 90º
- Ángulos desconocidos: α, β
Para saber qué valor tiene el ángulo α, podemos servirnos del seno:
Vemos que nos da un valor de 0,8. No obstante, ese no es el ángulo en grados. ¿Cómo podemos calcularlo? A través de la operación arcoseno o arcsin:
Por lo tanto, el ángulo α tiene un valor de 53,13º. Puedes realizar esta operación con la calculadora a través del operador arcsin o sin-1. Lo mismo sucede con las otras razones trigonométricas.
Sigamos el mismo proceso para determinar el valor del ángulo β. En este caso, nos serviremos de la tangente:
En resumen, los ángulos del triángulo rectángulo son:
- Ángulo rectángulo: 90º
- Ángulo α: 53,13º
- Ángulo β: 36,87º
Cálculo de los catetos a través del coseno y cosecante
Imaginemos ahora un triángulo rectángulo en el que conocemos todos los ángulos y la hipotenusa, pero no los catetos:
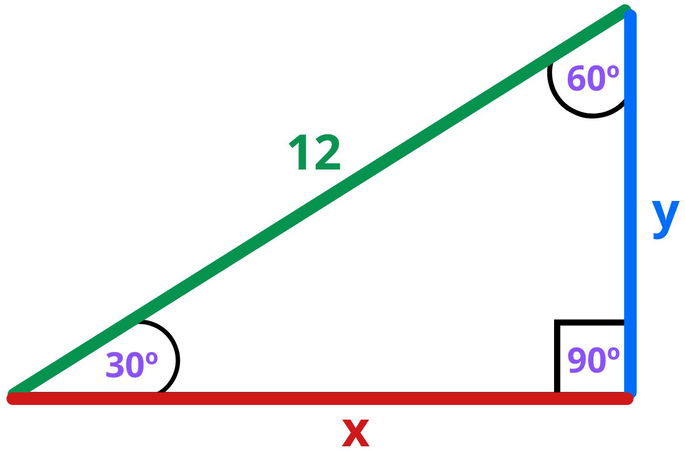
Sabemos lo siguiente:
- Hipotenusa: 12
- Ángulo recto: 90º
- Ángulo agudo inferior: 30º
- Ángulo agudo superior: 60º
- Incógnitas: cateto X, cateto Y
¿Cómo podemos calcular el valor de los catetos? Para ello, podemos utilizar las razones trigonométricas coseno y cosecante. Calculemos los catetos a partir del ángulo inferior, el de 30º.
Empecemos por calcular el cateto X usando el coseno:
Ahora calculemos el cateto Y usando la cosecante:
Por lo tanto, los valores de los catetos son:
- Cateto X: 10,39
- Cateto Y: 6
Vea también:
Cómo citar: (23/01/2024). "Razones trigonométricas". En: Significados.com. Disponible en: https://www.significados.com/razones-trigonometricas/ Consultado: