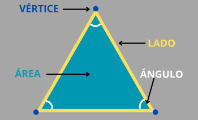
Triángulo rectángulo
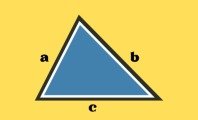
Un triángulo rectángulo es un triángulo que posee un ángulo de 90°. Es decir, es un polígono que consta de tres lados, tres vértices y tres ángulos, y uno de estos ángulos es recto.
Cada uno de los lados de esta figura geométrica recibe un nombre, a saber: catetos e hipotenusa.
Los catetos son los dos lados que forman el ángulo recto. La hipotenusa es el lado de mayor tamaño, y se encuentra opuesto al vértice del ángulo recto.

Una de las propiedades de los triángulos es que el conjunto de todos sus ángulos internos suman 180 grados. Si el ángulo recto mide 90°, la suma de los otros dos ángulos nunca superará los 90° que restan hasta los 180° totales. Esto significa que los otros dos ángulos han de ser agudos (inferiores a 90 grados) por necesidad.
Cuando los dos catetos miden lo mismo, los ángulos del triángulo son de las siguientes medidas: 90°, 45° y 45°, lo que da como resultado 180°.
Si los catetos tienen medidas diferentes, la amplitud de los ángulos agudos puede variar, pero nunca superar los 90°.
El perímetro del triángulo rectángulo se calcula sumando la medida de todos sus lados.
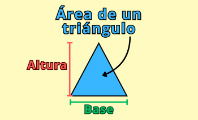
El área se halla multiplicando la longitud de la base del triángulo por la longitud de la altura, y dividiendo entre dos. Cabe aclarar que en este tipo de triángulo la base y la altura son los catetos, es decir, los segmentos que forman el ángulo recto.
Vea también Área de un triángulo.
Tipos de triángulo rectángulo y ejemplos
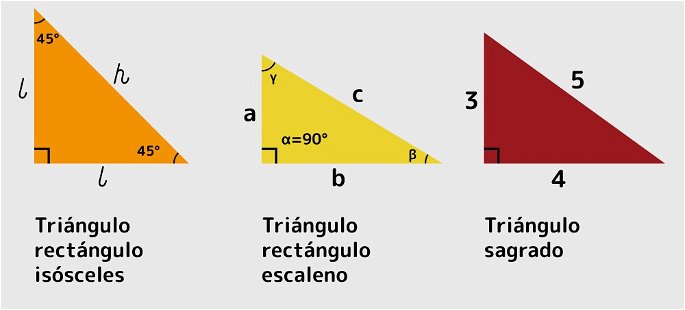
Los triángulos rectángulos pueden ser de dos tipos: isósceles o escalenos.
El triángulo rectángulo isósceles es aquel que, además de un ángulo de 90°, posee dos lados iguales, es decir, los dos catetos miden lo mismo.
El triángulo rectángulo escaleno presenta un ángulo de 90° y diferentes medidas en todos sus lados, por lo que también las medidas de sus ángulos serán todas diferentes.
El triángulo rectángulo sagrado, o de lados consecutivos, cuyos lados presentan medidas con relación 3, 4, 5. Es decir, estas medidas proporcionales permiten calcular las longitudes desconocidas de un triángulo rectángulo, simplificando las operaciones matemáticas necesarias. Este tipo de triángulo era muy utilizado por los egipcios y posteriormente recibió el nombre de triángulo pitagórico por su relación directa con el Teorema de Pitágoras.
Vea también Figuras geométricas.
Teorema de Pitágoras
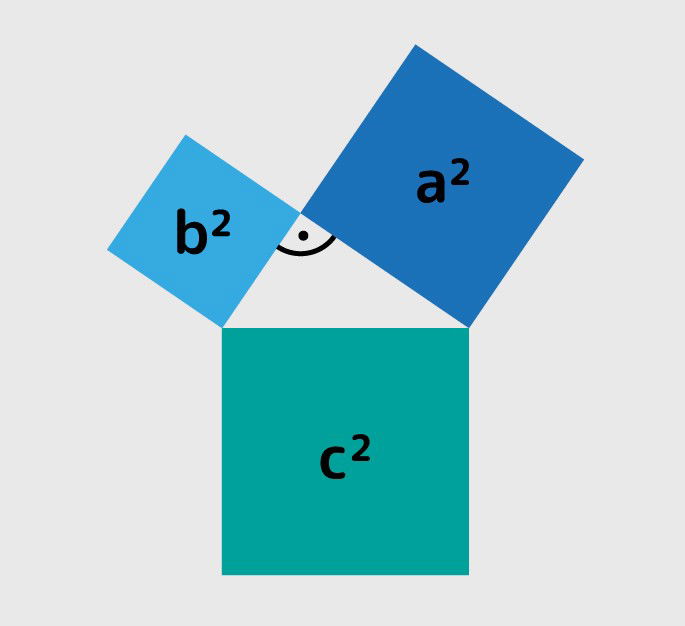
El Teorema de Pitágoras es un enunciado fundamental en geometría que establece las relaciones matemáticas entre los lados de un triángulo rectángulo, de esta forma:
En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
En esta fórmula, a y b hacen referencia a la longitud de los catetos y c a la longitud de la hipotenusa. El Teorema de Pitágoras es una herramienta muy práctica para hallar longitudes desconocidas de un triángulo rectángulo, es esencial en el campo de la geometría y muy aplicada en otras áreas de estudio.
Vea también:
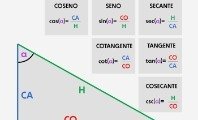
Razones trigonométricas
Las razones trigonométricas son herramientas esenciales para resolver problemas, comprender la relación entre los ángulos y los lados de un triángulo rectángulo, y se pueden utilizar para encontrar medidas desconocidas de ángulos y lados.
Seno
El seno de un ángulo es el cociente que resulta de dividir la longitud del cateto opuesto a ese ángulo y la longitud de la hipotenusa. Se representa como sin(θ), donde θ es el ángulo en consideración. Matemáticamente, se expresa como:
Donde co es un cateto opuesto; y h es la hipotenusa.
Coseno
El coseno de un ángulo en un triángulo rectángulo es la razón entre la longitud del cateto adyacente a ese ángulo y la longitud de la hipotenusa. Se representa como cos(θ). Matemáticamente, se expresa como:
Donde ca es un cateto adyacente; y h es la hipotenusa.
Tangente
La tangente de un ángulo se obtiene dividiendo la longitud del cateto opuesto a ese ángulo entre la longitud del cateto adyacente. Se representa como tan(θ). Matemáticamente, se expresa como:
Vea también Razones trigonométricas.
También te puede interesar:
Cómo citar: (29/02/2024). "Triángulo rectángulo". En: Significados.com. Disponible en: https://www.significados.com/triangulo-rectangulo/ Consultado: