Teorema de Pitágoras
El teorema de Pitágoras es una premisa matemática que nos permite calcular la longitud de los lados de un triángulo rectángulo.
El enunciado del teorema de Pitágoras dice lo siguiente:
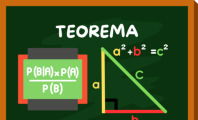
“En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos”.
La fórmula para calcular el teorema de Pitágoras es:
Las letras “a” y “b” representan los catetos del triángulo, y la letra “h” la hipotenusa.
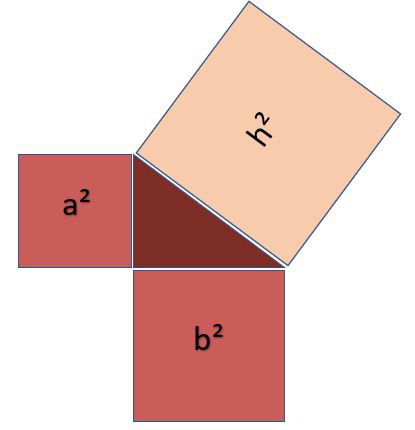
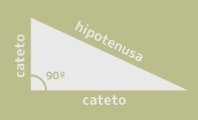
Un triángulo rectángulo es aquel que tiene un ángulo de 90°. Los dos lados que forman el ángulo recto se llaman catetos, el lado opuesto y más largo se llama hipotenusa.
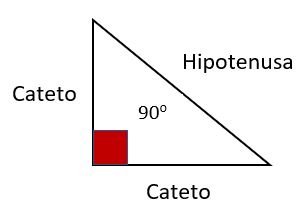
El teorema de Pitágoras solo es aplicable a este tipo de triángulos y para realizar el cálculo necesitamos conocer el valor de dos de los lados del triángulo.
Ejemplos del teorema de Pitágoras
A continuación presentamos un ejemplo que muestra un triángulo rectángulo del que conocemos la medida de los catetos, pero necesitamos hallar la medida de la hipotenusa. Vamos a explicar el proceso para encontrar el valor de la hipotenusa.
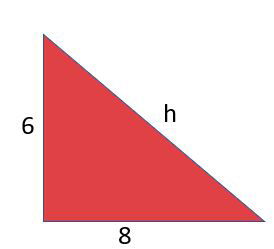
- Sabemos que los catetos del triángulo miden 6 y 8 respectivamente y necesitamos saber el valor de la hipotenusa
. - Para ello elevamos al cuadrado el valor de los catetos y los sumamos para saber cuánto vale el cuadrado de la hipotenusa
:
- Ya sabemos que , ahora necesitamos calcular la raíz cuadrada para conocer el valor de h:
En el siguiente ejemplo tenemos un triángulo rectángulo del que conocemos la medida de uno de los catetos y el valor de la hipotenusa. A continuación explicamos el proceso para calcular el valor del cateto desconocido.
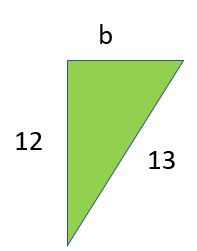
- Sabemos que uno de los catetos mide 12 y la hipotenusa 13.
- Para saber la medida del lado “b” elevamos los valores al cuadrado:
- Para hallar el valor de
tenemos que restar al cuadrado de la hipotenusa el cuadrado del cateto:
- El resultado es , así que tenemos que calcular la raíz cuadrada para saber el valor de
:
Vea también Hipotenusa.
Aplicaciones del teorema de Pitágoras
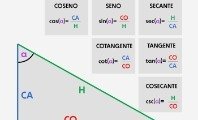
El teorema de Pitágoras es una herramienta básica en el estudio de la trigonometría. Permite conocer el área de cualquier tipo de triángulo a través de su división en triángulos rectángulos.
Gracias al teorema de Pitágoras se profundizó en el estudio de la geometría, lo que supuso un enorme avance para el conocimiento geográfico y la elaboración de mapas.
Esta premisa es fundamental en arquitectura e ingeniería. Permite definir y calcular distancias y medidas, necesarias en los proyectos de construcción.
El teorema de Pitágoras también se utiliza en medicina forense para determinar trayectorias, en sistemas de navegación y localización para calcular los puntos de ubicación y en disciplinas relacionadas con el diseño, como por ejemplo la confección textil.
Quién es Pitágoras
Pitágoras era un filósofo y matemático de la Antigua Grecia, nacido en la isla de Samos hacia el año 569 a. C.
Realizó su formación en los principales núcleos de conocimiento del Mediterráneo antiguo, Asia Menor y Egipto. Se formó como sacerdote geómetra, doctrina que interpreta el universo a través del número, y allí adquirió sus conocimientos matemáticos.
Fundó la hermandad Pitagórica en la ciudad de Crotona. Una escuela científica, filosófica y espiritual dedicada principalmente al estudio de los números y la geometría, aunque también trataban disciplinas como la música y la astronomía.
La hermandad sufrió un ataque, como consecuencia de su expansión y politización, que obligó a Pitágoras a huir a Metaponto, donde murió en el año 475 a. C.
Ver también:
- Qué es un teorema
- Qué es una fórmula
- Qué es la trigonometría
- Triángulo isósceles
- Triángulo rectángulo
- Triángulo equilátero
Cómo citar: (31/05/2023). "Teorema de Pitágoras". En: Significados.com. Disponible en: https://www.significados.com/teorema-de-pitagoras/ Consultado:
