Teorema de Tales
El teorema de Tales es uno de los teoremas que se aplican en matemáticas, específicamente en geometría. Se conoce como el teorema de proporcionalidad básica, e indica lo siguiente:
Si dos líneas transversales que parten de un mismo punto son interceptadas por varias rectas paralelas, en estas líneas se forman segmentos proporcionales. Para ilustrar esto, imaginemos que tenemos dos líneas que parten de un punto R, y son interceptadas por las rectas A y B.
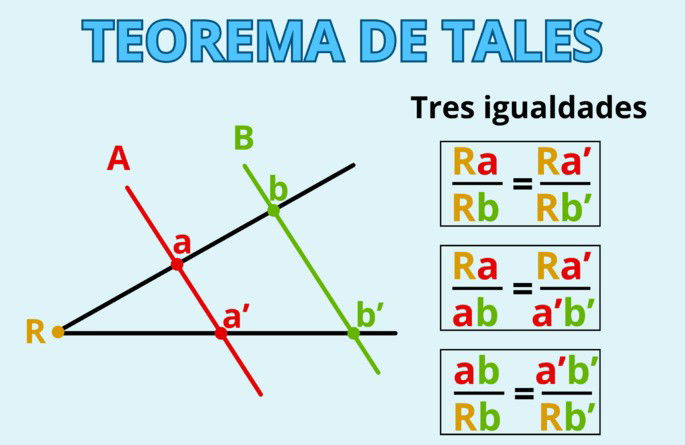
Podemos comprobar este teorema intercambiando las variables por valores conocidos. Supongamos que:
- el segmento Ra es de 2 metros de longitud,
- el segmento ab es de 4 metros de longitud,
- el segmento Ra' es de 3 metros de longitud,
- y el segmento a'b' es de 6 metros de longitud.
Si nos servimos de la segunda igualdad que mostramos en la imagen, tenemos:
Acabamos de comprobar mediante el teorema de Tales que todos los segmentos son proporcionales entre sí, ya que la razón o cociente entre los segmentos es la misma, de 0,5. Ten en cuenta que esto solo sucede cuando varias rectas paralelas (mantienen la misma distancia entre sí en todos los puntos) interceptan dos líneas que parten de un mismo punto.
Este teorema fue elaborado por Tales de Mileto, un filósofo griego que también tuvo influencia como matemático, físico y legislador.
Teorema de Tales en triángulos
El teorema de Tales tiene varias aplicaciones en el cálculo de los lados de triángulos semejantes. Un triángulo es semejante a otro cuando posee la misma forma, los ángulos inscritos son iguales y sus lados son proporcionales. Ahora, ¿cómo se forma un triángulo semejante?
Si dentro de un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que es semejante al triángulo original. Veamos la siguiente imagen:
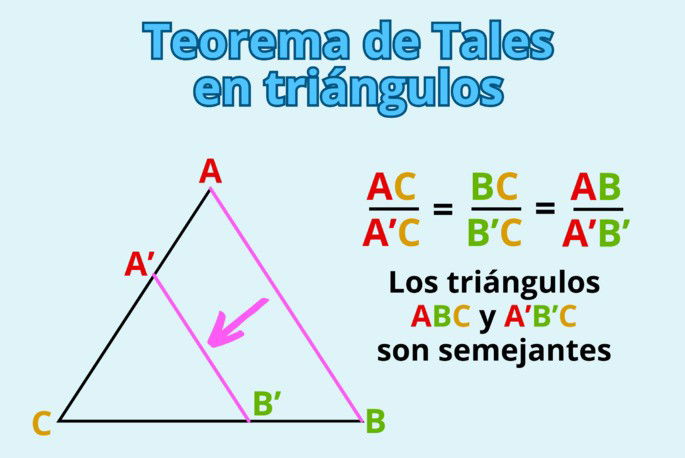
Se ha trazado una línea paralela al lado AB que dio lugar al lado A'B'. De esta forma, se presentan dos triángulos semejantes: el ABC, y el A'B'C.
El teorema de Tales nos dice que los lados de ambos triángulos son proporcionales entre sí. En otras palabras:
- el lado AC del triángulo original es proporcional al lado A'C del triángulo semejante;
- el lado BC del triángulo original es proporcional al lado B'C del triángulo semejante;
- el lado AB del triángulo original es proporcional al lado A'B' del triángulo semejante.
El ratio de proporcionalidad coincide en todos los casos, o sea, la proporción entre el lado AB y A'B' es la misma que entre los lados AC y A'C, y entre los lados BC y B'C.
Comprobemos esto con un ejemplo:
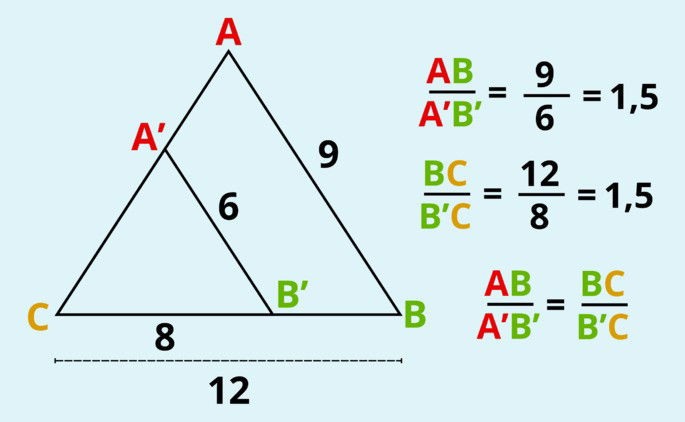
En los triángulos mostrados en la imagen, el lado AB tiene un valor de 9, mientras que el lado A'B' es de 6. Al hallar la razón o cociente entre ambos números, vemos que nos da 1,5.
De la misma forma, el lado BC posee un valor de 12, y el lado B'C, de 8. Si hacemos la división entre ambos números, comprobaremos que también obtenemos una razón de 1,5. Así pues, los triángulos de la imagen son semejantes, ya que se cumple el teorema de Tales.
Ejercicios del teorema de Tales
Aquí compartimos unos ejercicios para poner en práctica lo aprendido sobre el teorema de Tales.
Ejercicio 1
Dada la siguiente figura:
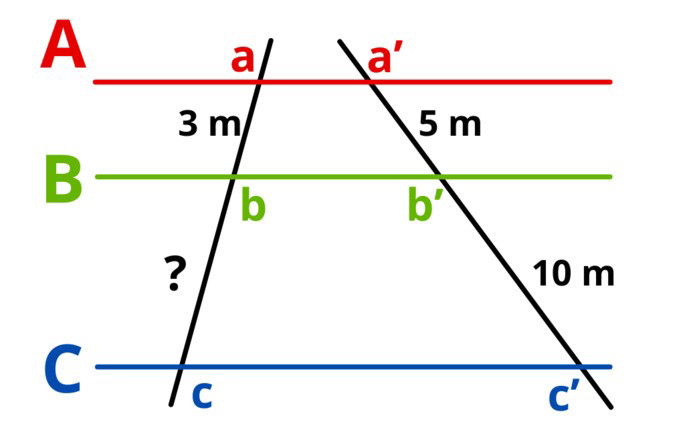
Encuentra la longitud del segmento bc.
Ejercicio 2
Observa la siguiente figura, cuyos lados se miden en centímetros:
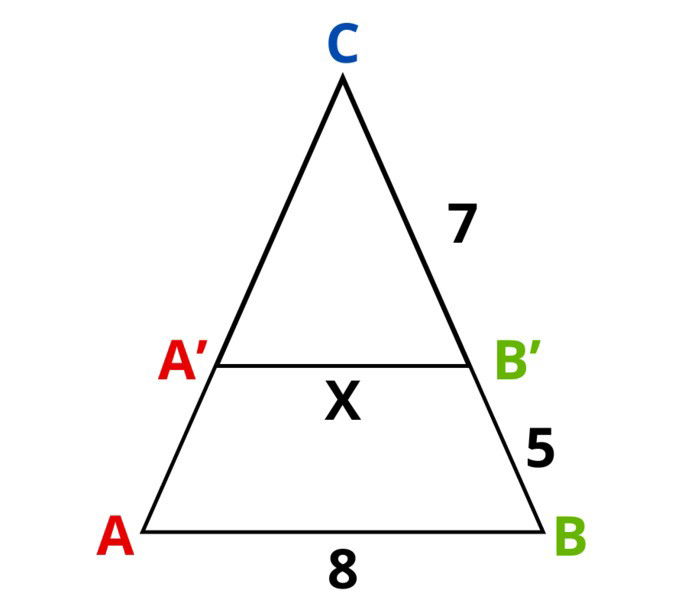
¿Cuál es el valor de X?
Ejercicio 3
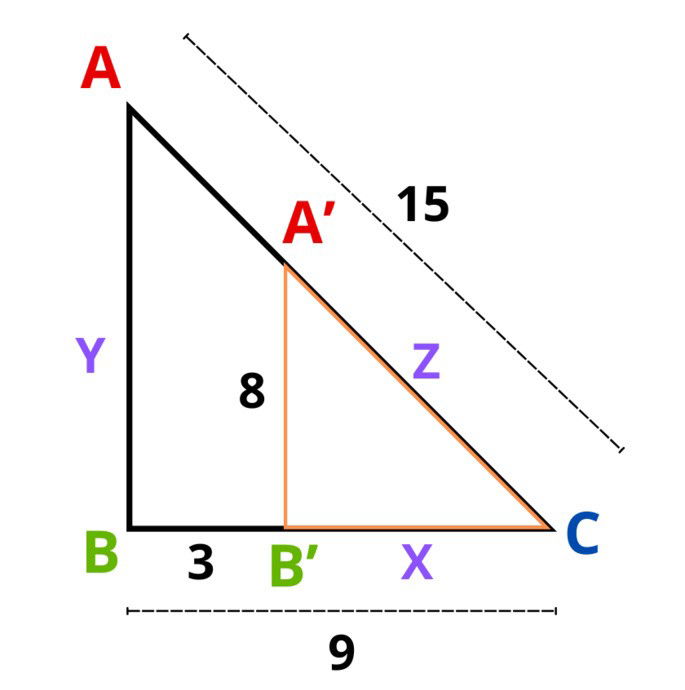
Halla el valor de las incógnitas X, Y y Z de la siguiente figura:
Ejercicio 4
¿Cuáles de las siguientes afirmaciones son correctas?
a) Según el teorema de Tales, las líneas transversales no tienen por qué ser cortadas por rectas paralelas.
b) Según el teorema de Tales, los segmentos formados por la intersección de líneas transversales y rectas paralelas son siempre proporcionales entre sí.
c) El teorema de Tales solo se aplica cuando dos rectas paralelas cruzan dos líneas transversales.
d) Un triángulo es semejante a otro cuando los ángulos inscritos son iguales y la forma es la misma, pero los lados no tienen por qué ser proporcionales.
e) Un triángulo es semejante a otro cuando los ángulos inscritos son iguales, la forma es la misma, y los lados son proporcionales
Vea también Teorema de Pitágoras y Teorema.
Cómo citar: Significados, Equipo (02/07/2025). "Teorema de Tales". En: Significados.com. Disponible en: https://www.significados.com/teorema-de-tales/ Consultado:
