Líneas Paralelas
Las líneas paralelas, o rectas paralelas, son dos líneas que siempre mantienen la misma distancia y si se prolongasen hacia el infinito nunca se tocarían. También se llaman líneas equidistantes porque, apuntando hacia la misma dirección, nunca llegan a tocarse.

Las líneas paralelas son un concepto fundamental en geometría que ha sido estudiado desde la antigüedad. Dos o más líneas que se encuentran en un mismo plano y que nunca se intersecan, sin importar cuánto se extiendan. Esta característica de no tocarse, a pesar de extenderse infinitamente, las hace únicas y les otorga propiedades geométricas particulares.
La importancia de las líneas paralelas radica en su aplicación en diversas áreas del conocimiento. Desde la construcción de edificios y la fabricación de objetos hasta el diseño gráfico y la programación, las líneas paralelas son una herramienta fundamental para crear estructuras estables, diseños simétricos y representaciones visuales precisas.
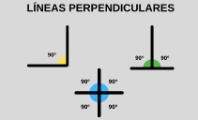
En matemáticas, es importante diferenciar las líneas paralelas de las líneas perpendiculares. Las rectas paralelas se acompañan en toda la trayectoria sin tocarse. Las líneas perpendiculares, en cambio, solo se encuentran en el punto donde se intersecan, creando un ángulo de 90 grados.
Cuando una recta transversal corta a dos rectas paralelas, se forman varios pares de ángulos que tienen la misma cantidad de grados.
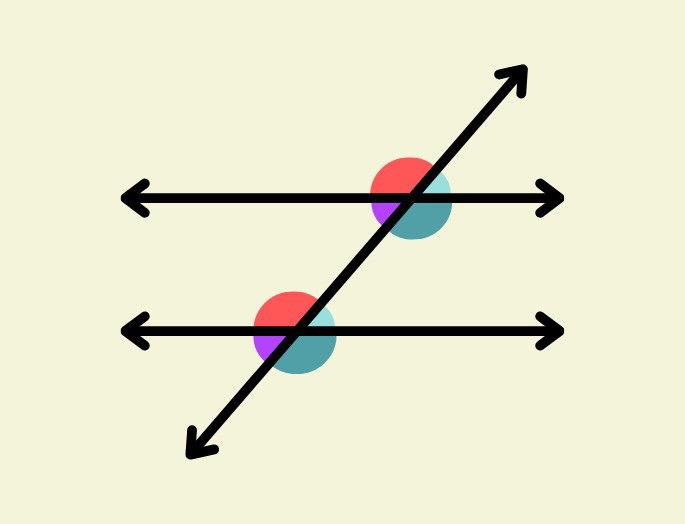
Los pares de ángulos son importantes para verificar si dos líneas son efectivamente paralelas, las siguientes condiciones deben cumplirse:
- Los ángulos correspondientes son iguales,
- Los ángulos interiores alternos son iguales,
- Los ángulos interiores consecutivos son suplementarios, es decir, suman 180 grados.
Características de las líneas paralelas
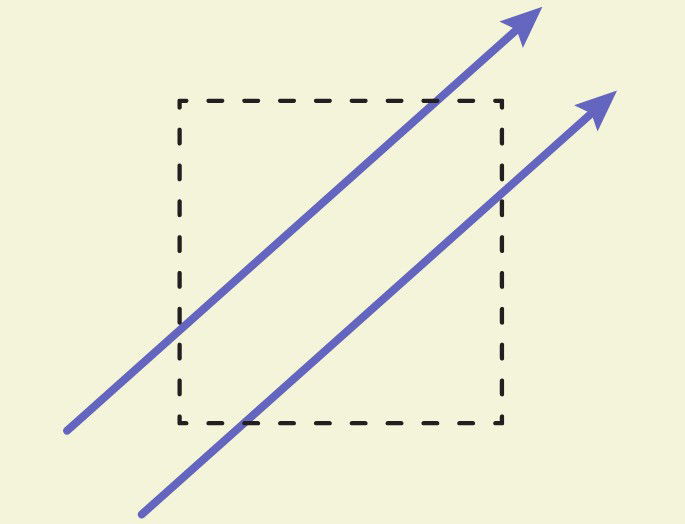
Equidistancia: las líneas paralelas siempre mantienen la misma distancia entre sí. Esto significa que si medimos la distancia perpendicular entre cualquier par de puntos correspondientes en las dos líneas, el valor obtenido será siempre el mismo.
No intersección: las líneas paralelas nunca se cruzan, ni siquiera en el infinito. Esta propiedad es la que define a las líneas paralelas y las diferencia de otras líneas, como las secantes o las perpendiculares.
Misma dirección: si prolongamos ambas líneas indefinidamente, seguirán manteniendo la misma dirección sin desviarse.
Ver también Qué es un Plano
Relación con otras líneas
Líneas perpendiculares: las líneas perpendiculares se intersecan formando un ángulo de 90 grados. A diferencia de las líneas paralelas, las perpendiculares siempre se cruzarán en un punto.
Líneas secantes: una línea secante es aquella que corta a otras líneas. Cuando una línea secante corta a dos líneas paralelas, se forman varios pares de ángulos con relaciones específicas (como los ángulos correspondientes, alternos internos y externos).
Teoremas y postulados
Postulado de las paralelas (o quinto postulado de Euclides).
Este postulado fue durante siglos objeto de estudio y debate entre matemáticos, ya que algunos consideraban que podía ser demostrado a partir de otros postulados. Establece que por un punto exterior a una recta, se puede trazar una única recta paralela a la dada.
A partir del postulado de las paralelas, se pueden demostrar numerosos teoremas relacionados con las líneas paralelas y los ángulos que se forman cuando una transversal las corta. Algunos de los teoremas más importantes son:
Teorema de los ángulos correspondientes: los ángulos correspondientes formados por una transversal que corta a dos líneas paralelas son iguales.
Teorema de los ángulos alternos internos: los ángulos alternos internos formados por una transversal que corta a dos líneas paralelas son iguales.
Teorema de los ángulos alternos externos: los ángulos alternos externos formados por una transversal que corta a dos líneas paralelas son iguales.
Teorema de los ángulos interiores consecutivos: los ángulos interiores consecutivos formados por una transversal que corta a dos líneas paralelas son suplementarios (suman 180 grados).
También puede ver:
Cómo citar: Significados, Equipo (14/08/2024). "Líneas Paralelas". En: Significados.com. Disponible en: https://www.significados.com/lineas-paralelas/ Consultado: