Área de un triángulo
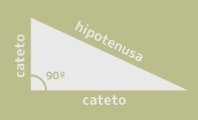
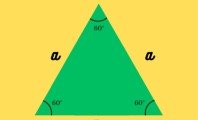
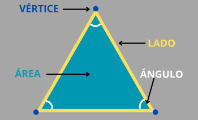
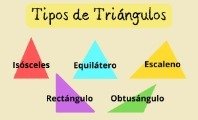
Un triángulo es una figura geométrica que tiene tres lados y tres ángulos. Según el tamaño de los lados y los ángulos que describen entre ellos, hablamos de un tipo de triángulo u otro, como triángulo rectángulo, escaleno, isósceles o equilátero.
En todos los casos, la fórmula básica para calcular el área es la misma:
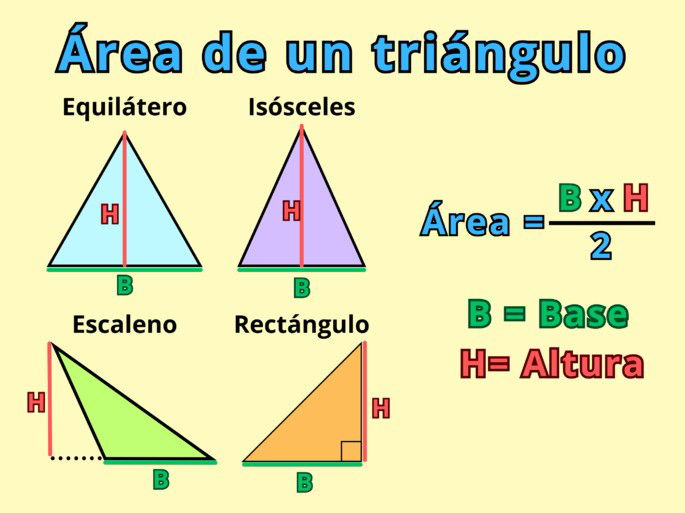
Es decir:
En el que:
- A es el área del triángulo, el espacio que ocupa en un plano;
- B es la base del triángulo, el lado en el que la figura se apoya;
- y H es la altura del triángulo, que es la recta que cruza desde el vértice más alto hasta la base, formando un ángulo de 90º.
Por tanto, el área de un triángulo es la base por la altura sobre dos, y se mide en unidades cuadradas, generalmente en cm2 (centímetros cuadrados) o m2 (metros cuadrados).
Otras fórmulas para sacar el área de un triángulo
Además de la fórmula básica para calcular el área del triángulo, existe otras maneras de obtener el mismo resultado. Dependiendo del tipo de triángulo y de los datos conocidos, podemos emplear las siguientes fórmulas.
En triángulos equiláteros
Un triángulo equilátero tiene todos los lados iguales. Podemos aprovechar esta propiedad para calcular el área de la siguiente forma:
En el que L corresponde a uno de los lados del triángulo equilátero. Por ejemplo, si hay un triángulo equilátero cuyos lados miden 7 centímetros de longitud, su área será:
Vea también Triángulo equilátero.
En triángulos isósceles
Un triángulo isósceles es aquel que posee dos lados iguales y una base de diferente tamaño. Es posible calcular el área de dicho triángulo sin conocer su altura:
En el que a corresponde a cada uno de los lados iguales, y b la base o el lado de diferente tamaño. Por ejemplo, si los lados de un triángulo isósceles miden 9 centímetros, y la base, 8 centímetros, entonces:
Vea también Triángulo isósceles.
En triángulos escalenos
Un triángulo escaleno es aquel en el que todos los lados y ángulos son diferentes entre sí. Para hallar el área, nos servimos de la fórmula de Heron:
En el que a, b y c son los distintos lados, y s el semiperímetro del triángulo. Para calcular el semiperímetro, basta con sumar todos los lados y dividir el resultado por 2.
Por ejemplo, tenemos un triángulo cuyos lados miden 4, 5 y 6 centímetros. Calculamos primero el semiperímetro:
Acto seguido, calculamos el área:
Vea también Triángulo escaleno.
En triángulos con solo dos lados y un ángulo conocidos
Para triángulos en que conocemos los lados a y b, y el ángulo α que se describe entre ellos, se utiliza la siguiente fórmula:
Por ejemplo, si un triángulo posee dos lados que miden 14 y 18 centímetros, respectivamente, que forman un ángulo de 33º, entonces:
Con todas estas fórmulas a tu disposición, podrás calcular el área de un triángulo, aunque no sepas todos los datos.
Ejercicios de cálculo del área de un triángulo
A continuación compartimos siete ejercicios para que practiques calculando el área de diferentes tipos de triángulos.
Ejercicio 1
Si un triángulo tiene una base de 5 centímetros, determina el área cuando la altura mide:
a) 4 centímetros.
b) 6 centímetros.
c) 9 centímetros.
Ejercicio 2
Determina el área de las siguientes dos figuras:
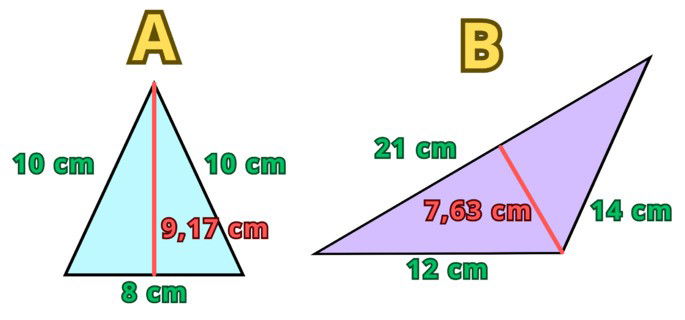
Ejercicio 3
Echa un vistazo al siguiente triángulo equilátero:
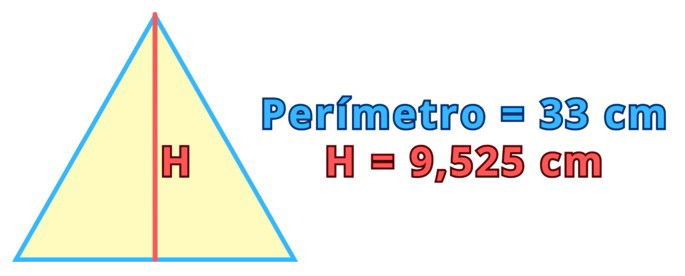
Calcula el valor de cada uno de los lados y el área de este triángulo.
Ejercicio 4
Determina la altura y el área del siguiente triángulo rectángulo:
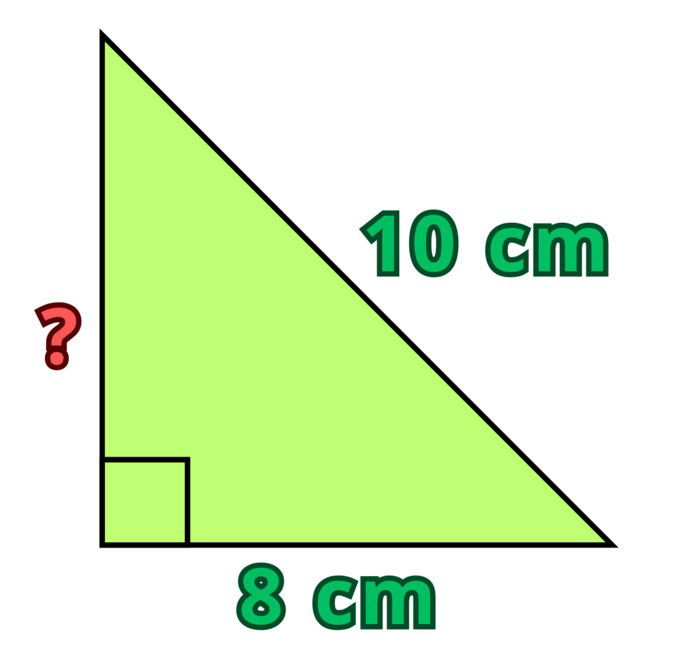
Ejercicio 5
Imagina que tenemos un triángulo equilátero de 3 centímetros de longitud en cada lado. ¿Cuál es el área de este triángulo?
Ejercicio 6
Calcula el área del siguiente triángulo:
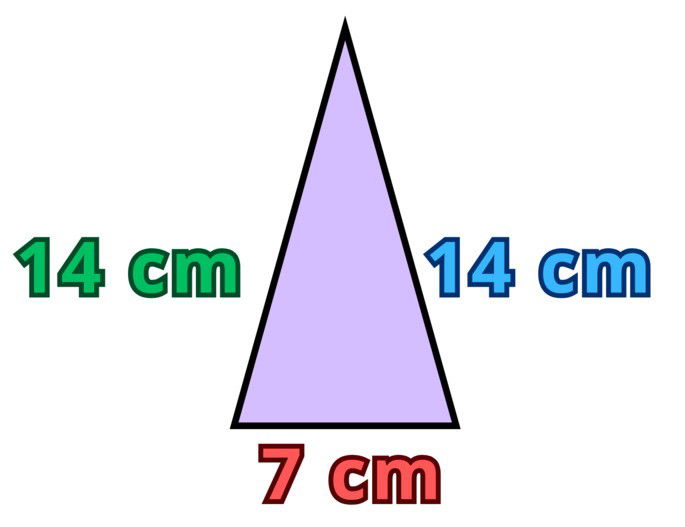
Ejercicio 7
En un triángulo conocemos los siguientes datos:
- Lado a = 7 cm
- Lado b = 8 cm
- Lado c = 13,5 cm
- Ángulo entre a y b = 52º
¿Cuál es el área del triángulo?
Vea también:
Cómo citar: Rhoton, Stephen (23/05/2025). "Área de un triángulo". En: Significados.com. Disponible en: https://www.significados.com/area-de-un-triangulo/ Consultado: