Aritmética
La aritmética es una rama de las matemáticas encargada del estudio de los números y las operaciones básicas que se pueden realizar con ellos, como sumar, restar, multiplicar y dividir.
A través de la aritmética podemos hacer cálculos y resolver ecuaciones simples. Saber cómo aplicarla a nuestro día a día nos ayuda a aprender a contar, medir, comparar y clasificar objetos o cantidades.
Por ejemplo, para una quedada de amigos y familiares, uno se encarga de comprar pollos para asar. Asumiendo que cada pollo asado da para 4 personas, y que en la quedada habrá 20 personas, podemos realizar una división para saber cuántos pollos comprar. O sea: 20 ÷ 4 = 5 pollos a comprar.
Otro ejemplo es cuando compartimos cuántos hermanos tenemos en total. Si uno tiene dos hermanos y una hermana, una simple suma nos bastará: 2 + 1 = 3 hermanos.
Como puedes ver, nos servimos de la aritmética en muchos ámbitos de la vida cotidiana, especialmente al calcular cantidades y tiempos. Además, también ejerce como una base sólida para el aprendizaje de otras disciplinas matemáticas, como el álgebra o la geometría.
Cabe mencionar que la aritmética solo cubre operaciones sencillas como sumas, restas, multiplicaciones, radicaciones, potencias, etc. Operaciones matemáticas como la derivación o las funciones son expresiones algebraicas.
Operaciones aritméticas
Las operaciones aritméticas son las diversas combinaciones que se efectúan con los números. Se clasifican en dos tipos de operaciones:
- en directas, que incluyen la suma, multiplicación y potenciación;
- e indirectas, que abarca la resta, división, radicación y logaritmo.
Operaciones aritméticas directas
Suma o adición (+)
La suma es la operación aritmética que consiste en la adición de dos o más números para obtener un resultado. Se representa mediante el símbolo más, +, y se puede utilizar para calcular una cantidad total de objetos o números.
Un ejemplo de una suma o adición es 4 + 2 = 6.
Vea también Suma.
Multiplicación (×, ·, *)
La multiplicación es una operación que se utiliza para encontrar el producto de dos factores (multiplicando y multiplicador). Consiste en la suma de un mismo número las veces que indique el multiplicador (3 × 2 = 3 + 3). Se representa mediante un símbolo de aspa (×), un punto (·) o un asterisco (*), como por ejemplo en a × b = p.
Un ejemplo de multiplicación es la siguiente operación aritmética: 7 x 3 = 21, que equivale a 7 + 7 + 7 = 21.
Vea también Multiplicación y Propiedades de la multiplicación.
Potenciación (nm)
Las potencias son operaciones que se utilizan para expresar el producto de factores iguales, con forma nm. Es decir, un número n, denominado base, es elevado a otro número m, denominado exponente.
La base se multiplica por sí misma tantas veces como diga el exponente. Por ejemplo, si tenemos 2 elevado a 4, o 24, el resultado es 24 = 16, pues es lo mismo que 2 x 2 x 2 x 2 = 16.
Vea también Leyes de los exponentes.
Operaciones aritméticas indirectas CONTINUAR AQUÍ
Resta o sustracción (-)
La resta es la operación que se utiliza para determinar la diferencia entre dos números y se representa mediante el símbolo menos (-). Un ejemplo de resta es 6 - 2 = 4.
Vea también Resta.
División (÷, /)
La división es la operación aritmética que se utiliza para dividir un número en partes iguales. Se representa con un número base, llamado dividendo, que es dividido por otro número, llamado divisor. El resultado de dicha operación se denomina cociente.
La división es la operación inversa de la multiplicación, por lo que, para comprobar si una división es correcta, podemos recurrir a la multiplicación. Por ejemplo: 6 ÷ 2 = 3, y si invertimos la operación, sería 3 x 2 = 6. La división es correcta.
Vea también División.
Radicación (n√)
La raíz de un número (√) es la operación aritmética inversa a la potenciación y se utiliza para encontrar la raíz cuadrada o de orden n. Por ejemplo, la raíz cuadrada de 25 es: √25 = 5, ya que 5² = 25 o 5 × 5 = 25.
Vea también Raíz cuadrada.
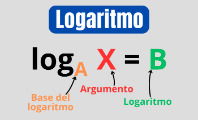
Cálculo de logaritmos
El logaritmo es una operación que se utiliza para hallar el exponente al que hay que elevar una base para obtener un determinado número. Se representa como log seguido el número que representa la base como subíndice, y entre paréntesis el número cuyo logaritmo hemos de calcular.
Por ejemplo, log2 (8) = 3, ya que 2 elevado a la tercera potencia es igual a 8 (23 = 8).
Vea también Logaritmo.
Ejemplos de aritmética
Aquí tenemos más ejemplos de aritmética que combinan los tipos de operaciones que cubre esta rama de las matemáticas:
Suma: 4 + 2 + 3 = 9
Resta: 4 - 2 - 3 = -1
Suma y resta: 5 - 6 + 7 = 6
Multiplicación: 3 × 4 = 12
Resta, suma y multiplicación: 12 - 4 + 2 x 3 = 14
Suma y potenciación: 23 + 52 = 8 + 25 = 33
Divisiones y resta: 9 ÷ 3 - 8 ÷ 4 = 3 - 2 = 1
Suma de raíces: √100 + 3√8 = 10 + 2 = 12
Logaritmo: log5 (25) = 2
Multiplicación, logaritmo y resta: 3 x log4 (64) - 5 = 3 x 3 - 5 = 4
Origen e historia de la aritmética
La aritmética es una de las ramas más antiguas de las matemáticas que se remonta a miles de años atrás. Su origen se sitúa en Mesopotamia, en torno al año 2000 a. C., donde babilonios y los sumerios desarrollaron el sistema numérico sexagesimal. Dicho sistema continúa en uso para medir, por ejemplo, el tiempo o los ángulos.
En Egipto y en la Antigua Grecia se llevaron a cabo grandes hallazgos en materia aritmética. No obstante, fue durante la Edad Media cuando los matemáticos árabes desarrollaron el sistema numérico decimal, a partir de uno heredado de la cultura hindú. Un sistema posicional de base 10, inicialmente contaba con las cifras del 1 al 9, hasta que se creó el símbolo para representar la posición 0. Está integrado por los dígitos que se utilizan actualmente y sirve para representar cualquier número.
Vea también:
Referencias:
Bressan, O. J. (2007). Los números y las operaciones Aritméticas. El Recuperado vol. 31.
Gálvez, Adriana María; Maldonado, Andrés Felipe; Guacaneme, Edgar Alberto (2012). ¿A qué llamamos historia de la aritmética? Una respuesta a través de cinco trazas. En Obando, Gilberto (Ed.), Memorias del 13er Encuentro Colombiano de Matemática Educativa (pp. 347-352). Medellín: Sello Editorial Universidad de Medellín.
Cómo citar: Significados, Equipo (09/09/2025). "Aritmética". En: Significados.com. Disponible en: https://www.significados.com/aritmetica/ Consultado: