Funciones matemáticas
Una función matemática o función en cálculo es una relación que se establece con una variable que depende de otra. O sea, una magnitud es función de otra si el valor de la primera depende del valor de la segunda.
En otras palabras, una función relaciona una variable dependiente, es decir, que depende de otra variable, con una variable independiente. La variable independiente es la que cambia de valor para determinar qué magnitud presentará la variable dependiente.
De forma algebraica, la función se expresa o se denota de la siguiente forma:
f: A → B
En el que:
- f es la función;
- A corresponde al dominio de la función f o el conjunto de elementos de partida;
- y B al codomonio de la función o el conjunto de llegada.
Del codominio B surge las imágenes de la función, que son los valores relacionados con elementos del dominio A. Por ejemplo, digamos que a la función y = 2x denotamos el dominio A, o x, como los números naturales del 2 al 6, y el codominio B, o y, como los números pares del 2 al 16.
Podemos elaborar entonces la siguiente tabla:
| Valor de x en dominio A | Imagen de la función | Elementos del codominio B |
|---|---|---|
| - | - | 2 |
| 2 | 4 | 4 |
| 3 | 6 | 6 |
| 4 | 8 | 8 |
| 5 | 10 | 10 |
| 6 | 12 | 12 |
| - | - | 14 |
| - | - | 16 |
En el ejemplo, los valores 2 al 6 del dominio A son la variable independiente, pues es el valor que modificamos para que nos dé la imagen de la función. A su vez, las imágenes corresponden a elementos del B relacionados con A, y podemos fijarnos en que quedan elementos del B sin asociarse.
Usualmente, la operación de la función se representa con f(x) o con g(x), que en los gráficos equivale al eje de ordenadas o y.
Tipos de funciones matemáticas
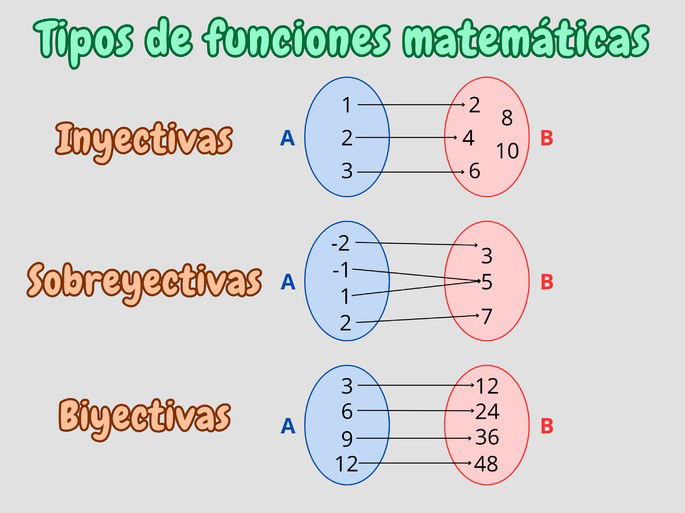
Las funciones matemáticas se clasifican en tres tipos principales según la relación entre los elementos del dominio A y el codominio B.
1. Funciones inyectivas
Las funciones inyectivas son aquellas en que a cada elemento del dominio A le corresponde un elemento en B. A su vez, ningún elemento de A comparte con otro elemento una misma imagen en B, y puede haber elementos en B que no se relacionen con ningún elemento en A.
2. Funciones sobreyectivas
También denominadas funciones subyectivas, aquí todo elemento del codominio B es una imagen de por lo menos un elemento del dominio A. Por tanto, se diferencia de la inyectiva en que nunca quedan elementos en B sin relacionarse con elementos en A.
3. Funciones biyectivas
Una función biyectiva es a la vez una función inyectiva y sobreyectiva. A raíz de esto, a cada elemento del dominio A le corresponde a un único elemento en el codominio B, y no quedan imágenes sin asociar. Por tanto, el dominio A y el codominio B presentan el mismo número de elementos.
Otros tipos de funciones matemáticas
Además de las funciones inyectivas, sobreyectivas y biyectivas, existen diversos tipos de funciones según los términos que las componen.
Funciones constantes
Son aquellas descritas como f(x) = a, en que a es una constante. Como para todo valor de x siempre se obtiene la misma imagen (el valor dado por a), la función se representa en una gráfica como una recta horizontal paralela al eje de abscisas o de x.
Un ejemplo de una función constante es f(x) = 5, pues para todo valor de x, la función siempre dará la misma imagen, que es 5.
Funciones afines
Son funciones polinómicas de primer grado que no pasan por el origen de coordenadas. Se representan como f(x) = ax + b, en que:
- a es el coeficiente de la variable x, que determina la inclinación o ángulo de la recta en el gráfico;
- y b es una constante que marca el punto de intersección de la recta con el eje de abscisas y ordenadas.
Un ejemplo de una función afín es f(x) = 4x + 3.
Vea también Ecuación de primer grado.
Funciones lineales
Son un caso concreto de las funciones afines, en que el valor de b es igual a 0. Por tanto, la recta siempre interseca por el origen de las coordenadas, y se representa como f(x) = ax. Un ejemplo es f(x) = 2x.
Dentro de las funciones lineales, podemos hablar también de la función identidad, en que el coeficiente a es igual a 1. Por tanto, la función se denota como f(x) = x.
Funciones cuadráticas
Son funciones polinómicas de segundo grado, es decir, f(x) = ax2 + bx + c, en que a ha de ser diferente de 0. Los elementos a, b y c son coeficientes o constantes que pueden tomar tanto valores positivos como negativos.
Un ejemplo de función cuadrática es f(x) = 6x2 - 3x + 1.
Vea también Ecuaciones de segundo grado.
Funciones polinomiales
Las funciones polinomiales engloban las afines, las cuadráticas y todas aquellas de tercer o mayor grado. Podemos representar este tipo de funciones de la siguiente forma:
f(x) = anxn + an–1xn–1 + ... + a1x1 + a0
En el que n es un número entero, cuyo valor indica el grado de la función polinomial. Por ejemplo, f(x) = -4x3 + 2x +9 es una función polinomial cúbica o de tercer grado.
Funciones logarítmicas
Una función logarítmica se denota como f(x) = loga x, en que a es una base real positiva diferente de 1. En lugar de x, puede haber otras expresiones como un polinomio.
Un ejemplo de función logarítmica es f(x) = loga (8x + 3).
Funciones exponenciales
Una función exponencial es aquella representada como f(x) = ax, en que a ha de ser diferente de 0. Igual que con la función logarítmica, en lugar de x puede haber otras expresiones algebraicas.
Funciones trigonométricas
También llamadas funciones circulares, son aquellas relacionadas con la circunferencia trigonométrica. Aquí, la variable independiente es la medida de un ángulo, que a su vez es la razón entre catetos e hipotenusa de un triángulo descrito dentro de la circunferencia.
De aquí surgen los conceptos como seno, coseno, tangente, secante, cosecante y cotangente. Tres ejemplos de funciones trigonométricas son:
- Función seno: f(x) = sen x
- Función coseno: f(x) = cos x
- Función tangente: f(x) = tg x
Cabe mencionar que todas las funciones trigonométricas son periódicas, o sea, se repiten en intervalos definidos.
Vea también Funciones trigonométricas.
Funciones inversas
Una función inversa es la función recíproca de otra que puede invertirse. Por ejemplo, si en una función tomamos valores del dominio A, la función transformará estos valores en imágenes contenidas en el codominio B. La función inversa es tomar valores del codominio B que dan lugar a imágenes contenidas en el dominio A.
Funciones pares
Una función par es aquella en que se cumple la igualdad f(-x) = f(x). En otras palabras, la función genera una misma imagen tanto para x como para -x.
Funciones impares
Son aquellas en que se cumple la igualdad f(-x) = -f(x). En este caso, se genera un gráfico simétrico con respecto al origen de coordenadas.
Funciones modulares
Una función modular es aquella cuya imagen es siempre un valor positivo, y se representa como f(x) = |x|.
Funciones racionales
Son funciones que resultan del cociente de dos funciones polinomiales, y se representa de la siguiente forma:
Ejemplos de funciones matemáticas
A continuación presentamos unos ejemplos de expresiones matemáticas que también son funciones.
Un primer ejemplo es la ecuación que relaciona la fuerza con la masa y aceleración, es decir, F = m·a. La fuerza es la variable dependiente, representado como f(x) o y, mientras que la masa y la aceleración son variables independientes. Por tanto, el valor de la fuerza cambia en función de los valores de la masa o la aceleración.
El cálculo del área de una figura geométrica es otro ejemplo. Tomemos el caso de un círculo, cuyo área es A = π·r2. Aquí la variable dependiente es el área, cuyo valor cambia en función de la magnitud de r, que es el radio del círculo.
Otro ejemplo es la velocidad, que se calcula en función de la distancia recorrida en un tiempo determinado: v = d / t. Al modificar la magnitud de la distancia o tiempo, el valor de la velocidad cambia en consecuencia.
Por último, otro ejemplo de función es el teorema de Pitágoras, que establece la relación entre la hipotenusa, h, y los catetos a y b como h2 = a2 + b2. Cuando la magnitud de uno de los catetos varía, cambia también el valor de la hipotenusa, pues es la variable dependiente.
Vea también Ecuaciones y Matemáticas.
Cómo citar: Significados, Equipo (26/06/2025). "Funciones matemáticas". En: Significados.com. Disponible en: https://www.significados.com/funciones-matematicas/ Consultado: