Números imaginarios
Los números imaginarios son un conjunto que forma la parte imaginaria de los números complejos. En concreto, abarca aquellos números que contengan la unidad o constante imaginaria, i, que equivale a √−1.
Por ejemplo, 5i es lo mismo que 5 x √−1, mientras que i√81 es igual a √−1 x √81. Por tanto, los números imaginarios son aquellos que incluyen el término de la raíz cuadrada de −1, y se representan como Bi, en que B es un número real diferente de 0.

Los números imaginarios surgieron a partir de buscar una solución a x2 + 1 = 0. Al transformar esta ecuación como x2 = −1 → x = √−1, podemos ver que la solución no es un número real, ya que no existe la raíz cuadrada de un número real negativo. Debido a esto, se introdujo la idea de los números imaginarios para tratar con este caso y con cualquier raíz cuadrada de un número negativo.
El concepto de los números imaginarios surgió en XVII. Sin embargo, no fue hasta el siglo XVIII y XIX que ganó aceptación entre los matemáticos, gracias a los trabajos de Augustin Louis Cauchy, Carl Friedrich Gauss y en especial Leonhard Euler. Otros matemáticos destacados fueron Raffaele Bombelli, Gerolamo Cardano, Caspar Wessel y Jean-Robert Argand.
Los números imaginarios tienen varias tiene aplicaciones en la ingeniería eléctrica, en las telecomunicaciones y en algunas ramas de la física, como la física cuántica. Es común servirse de ellos al describir las funciones de onda o estudiar fenómenos ondulatorios, así como en la mecánica de fluidos y procesado de señales.
Generalmente, estos números se representan con el símbolo i. En algunos casos, como en la ingeniería eléctrica, se representan con la letra j.
Características de los números imaginarios
Los números imaginarios forman parte solamente del conjunto de los imaginarios y los complejos. Otros conjuntos, como el de los reales, fraccionarios o enteros, no incluyen números imaginarios.
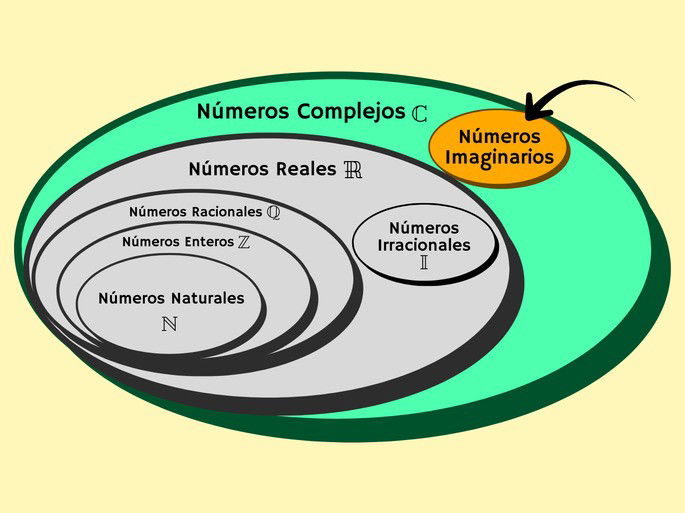
Los números imaginarios son un componente de la parte imaginaria de los números complejos. Recuerda que los números complejos presentan una estructura de Re(Z) + Im(Z) o A + Bi. En este caso, tanto Im(Z) como Bi corresponden a la parte imaginaria.
Entonces, los números imaginarios se componen de un coeficiente real B y la unidad imaginaria i. A raíz de esto, un número imaginario existe solamente si el coeficiente real es diferente de 0.
En el plano de los números complejo o plano complejo, los números imaginarios se representan en un eje vertical llamado eje imaginario. Este eje es perpendicular al horizontal que corresponde a los números reales, y su unidad es igual a la unidad imaginaria i.
Existe un número infinito de números imaginarios puros, pues a la unidad imaginaria i podemos multiplicar cualquier número real. Recuerda que el número imaginario contiene la unidad imaginaria i multiplicada por un número real B.
Una última característica a destacar es que los números imaginarios no pueden atribuirse a valores ordinales, es decir, no se pueden ordenar de acuerdo con su valor. Esta es una de las grandes diferencias con los números reales, que sí se pueden ordenar según sus valores.
Ejemplos de números imaginarios
Un ejemplo de número imaginario es la unidad imaginaria con signo negativo, es decir, −i. Esto es igual a multiplicar -1 a la unidad imaginaria, lo que resulta en −1 x √−1 = −1 x i = −i.
Otros ejemplos de números imaginarios son 3i, 24i, 7,42i y -15i. Por tanto, la parte imaginaria de un número complejo puede incluir números naturales, enteros negativos o cifras con decimales que multiplican la unidad imaginaria.
La unidad imaginaria también se puede multiplicar a números fraccionarios, con raíces o exponentes, como:
Otra posibilidad es multiplicar la unidad imaginaria con expresiones algebraicas, como las siguientes:
- (4x + 2) x i
- (3x2 - 5x + 7) x i
- (-6y + sen(x) - √4) x i
Por último, es posible realizar operaciones aritméticas con varias unidades imaginarias, como:
- 4i + 2i = (4 + 2)i = 6i
- 3i x 4i = (3 x 4)i2 = 12i2 = 12 x (−1) = −12
- 2i2 x 4i3 = (2 x 4)i5 = 8i5 = 8 x (−1) x (−1) x i = 8i
Vea también:
Cómo citar: Significados, Equipo (07/10/2025). "Números imaginarios". En: Significados.com. Disponible en: https://www.significados.com/numeros-imaginarios/ Consultado: