Números
Los números son un concepto fundamental en matemáticas y ciencia, se utilizan para representar cantidades, ordenar elementos o identificar posiciones. Desde los tiempos más antiguos, los números han sido empleados como herramientas para contar, medir y realizar cálculos, jugando un papel crucial en el desarrollo de la civilización.

Un número es una entidad abstracta que describe una cantidad o magnitud. Puede definirse de diversas maneras según el contexto matemático o científico. En términos simples, es un símbolo que expresa una cantidad. Por ejemplo, 3 representa una cantidad de tres unidades.
Los números tienen múltiples aplicaciones en la vida cotidiana y en diversas disciplinas. En matemáticas, son esenciales para realizar operaciones aritméticas (suma, resta, multiplicación, división). En la vida diaria, permiten medir distancias, tiempo, dinero y muchos otros aspectos. En otras ciencias, son fundamentales para formular leyes, realizar mediciones y desarrollar modelos.
Clasificación y tipos de números
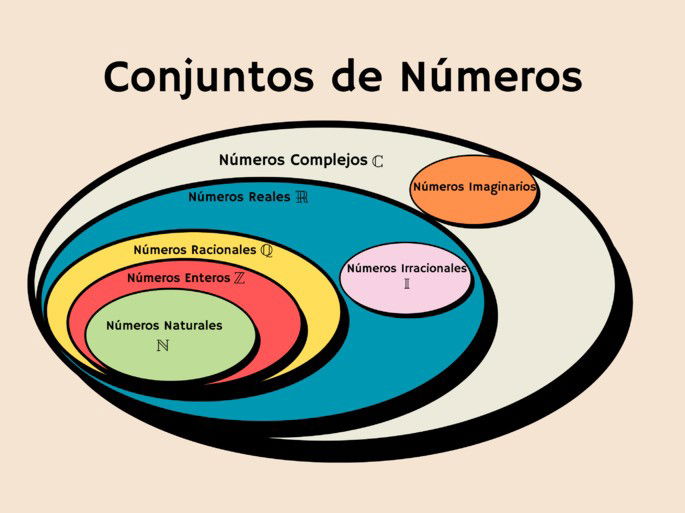
Los números se clasifican en diferentes tipos, dependiendo de sus propiedades y su uso en las matemáticas. Entre los principales tipos de números encontramos:
Números naturales (N)
Los números naturales se emplean para tareas fundamentales como contar objetos y ordenar elementos. Representan cantidades enteras no negativas, y su conjunto es infinito:
Los números naturales pueden ser cardinales, cuando se utilizan para contar (por ejemplo, el número de personas en una sala). Y ordinales, cuando sirven para indicar la posición de un elemento en un orden (por ejemplo, el primer lugar en una carrera).
Ver también Números Naturales
Números enteros (Z)
Son una extensión de los números naturales, pues incluyen los números naturales, sus negativos y el cero:
Los números enteros permiten contar cantidades que representan deudas o déficit (números negativos), así como ganancias o incrementos (números positivos).
Se utilizan también para definir posiciones por encima o por debajo de un punto de referencia, como las temperaturas (por encima o por debajo de cero) o los pisos de un edificio.
Saber más sobre Números Enteros
Números racionales (Q)
Son aquellos que pueden expresarse como fracción de dos números enteros, donde el denominador no es cero. Ejemplo: 1/2, 3/4.
Un número racional puede ser una fracción o un número decimal. Dependiendo de cómo se exprese, un número racional puede clasificarse como:
-
Decimal exacto: cuando su expansión decimal es finita. Ejemplo
-
Decimal periódico puro: cuando su expansión decimal tiene una repetición infinita de dígitos. Ejemplo:
-
Decimal periódico mixto: cuando hay una parte no repetitiva antes del periodo repetitivo. Ejemplo:
Ver también Número Racionales
Números irracionales (I)
Los números irracionales son aquellos que no pueden expresarse como el cociente de dos enteros, es decir, no pueden escribirse como fracciones. Su expansión decimal es infinita y no periódica. Algunos ejemplos son:
Estos números suelen aparecer en situaciones geométricas, como la longitud de la diagonal de un cuadrado o de la circunferencia de un círculo.
Saber más sobre Números Irracionales
Números reales (R)
Conjunto de números que agrupa tanto a los números racionales como a los irracionales. Es decir, todos los números que pueden representarse en la recta numérica son números reales:
Los números reales abarcan todas las cantidades continuas que se pueden medir, por lo que son fundamentales en la física y otras ciencias.
Ver también Números Reales
Números imaginarios
Los números imaginarios surgen cuando se necesita trabajar con raíces de números negativos. El número imaginario básico es i, definido como la raíz cuadrada de -1:
Los números imaginarios son esenciales en muchos campos de la física y la ingeniería, especialmente en el análisis de señales y sistemas complejos.
Números complejos (C)
Los números complejos son una extensión de los números reales, y se forman al combinar un número real con un número imaginario. Un número complejo tiene la forma:
Donde a es la parte real y b es la parte imaginaria. Por ejemplo, este sería un número complejo:
Estos números son fundamentales en áreas avanzadas de matemáticas, como en la resolución de ecuaciones polinómicas de grado superior y en la teoría cuántica.
Vea también Números complejos.
Historia de los números

El origen del uso de los números se remonta a la prehistoria, cuando los primeros seres humanos contaban utilizando objetos como piedras, palos y sus propios dedos. Estas primeras herramientas de conteo evolucionaron en los sistemas numéricos que conocemos hoy.
Con el paso del tiempo, las civilizaciones antiguas desarrollaron sistemas de numeración más sofisticados. Los egipcios, por ejemplo, utilizaban un sistema decimal que constaba de un símbolo que representaba la decena (una U invertida). Mientras que los romanos crearon un sistema basado en letras que empleaba solo siete símbolos (I, V, X, L, C, D y M) y que aún hoy en día se utiliza en relojes y monumentos. Sin embargo, estos sistemas tenían limitaciones a la hora de realizar cálculos complejos.
Fue en la India donde se produjo una verdadera revolución en la historia de los números. Los matemáticos hindúes introdujeron dos conceptos fundamentales: el valor posicional y el cero. El valor posicional significa que el valor de un dígito depende de la posición que ocupa dentro de un número. El cero, por su parte, representa la ausencia de cantidad y es esencial para nuestro sistema de numeración decimal.
Los árabes adoptaron y perfeccionaron el sistema numérico hindú, difundiendo sus conocimientos por todo el mundo. Los números indoarábigos, como los conocemos hoy en día, llegaron a Europa gracias a matemáticos como Leonardo Fibonacci, quien los popularizó en su obra "Liber Abaci".
A medida que avanzaba la matemática, los números se volvieron cada vez más abstractos y complejos. Los matemáticos descubrieron los números negativos, los números imaginarios y los números complejos, que permitieron resolver problemas que antes se consideraban imposibles.
Ver también:
Referencias:
Suárez, M. (2004). Interaprendizaje holístico de matemática. Ibarra, Ecuador: Gráficas Planeta.
Morales, G. L. R., & Hernández, V. F. R. (2001). ¿Qué es el número? CIENCIA ergo-sum, 8(1), 111-118.
Cómo citar: Significados, Equipo (27/09/2024). "Números". En: Significados.com. Disponible en: https://www.significados.com/numeros/ Consultado:









